Question

ΔPQR असा काढा की PQ - PR = 2.4 सेमी, QR = 6.4 सेमी आणि ∠PQR = 55°.

Answer 1

कच्ची आकृती:

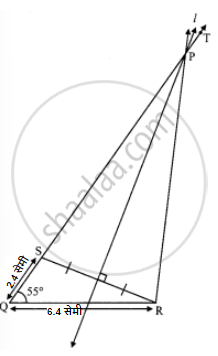
स्पष्टीकरण:

PQ - PR = 2.4 सेमी

∴ PQ > PR

QR हा रेषाखंड काढू. रेख QR शी 55° कोन करणारा किरण QT काढता येतो.

त्या किरणावर S बिंदू शोधायचा आहे. QS = 2.4 सेमी असा S बिंदू त्या किरणावर घेतला.

आता, PQ – PS = QS    ...[Q-S-P]

∴ PQ – PS = 2.4 सेमी      ...(i)

तसेच, PQ – PR = 2.4 सेमी    ...(ii) [दिलेले]

∴ PQ – PS = PQ – PR    ...[(i) आणि (ii) वरून]

∴ PS = PR

∴ बिंदू P हा रेख RS च्या लंबदुभाजकावर आहे.

∴ बिंदू P हा किरण QT चा छेदनबिंदू आहे आणि रेख RS चा लंबदुभाजक आहे.

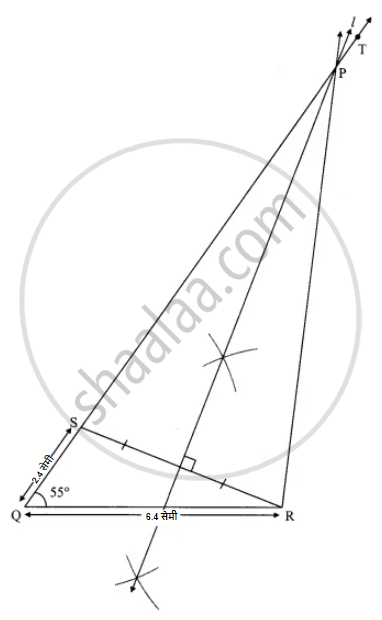
रचनेच्या पायऱ्या:

1. रेख QR हा 6.4 सेमी काढा.
2. Q बिंदूपाशी 55° कोन करणारा किरण QT काढा.
3. किरण QT वर D बिंदूअसा घ्या की QS = 2.4 सेमी.
4. रेख SR काढून त्याचा लंबदुभाजक काढा.
5. रेख SR चा लंबदुभाजक किरण QT ला जेथेछेदतो त्या बिंदूला P नाव द्या.
6. रेख PR काढा.

ΔPQR हा अपेक्षित त्रिकोण आहे.