Advertisements
Advertisements
प्रश्न
Read the following paragraph and answer the questions.
|
Consider the experimental set-up shown in the figure. This jumping ring experiment is an outstanding demonstration of some simple laws of Physics. A conducting non-magnetic ring is placed over the vertical core of a solenoid. When current is passed through the solenoid, the ring is thrown off. |
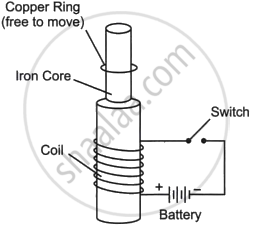
- Explain the reason for the jumping of the ring when the switch is closed in the circuit.
- What will happen if the terminals of the battery are reversed and the switch is closed? Explain.
- Explain the two laws that help us understand this phenomenon.
उत्तर
- When a switch in a circuit is closed, current flows, causing emf in the circuit. The magnetic field of the solenoid varies continually due to ac. This causes an eddy current to form in the ring. The magnetic field produced by the induced eddy current in the ring, according to Lenz's law, opposes the changing magnetic field of the solenoid. As a result, the two magnetic fields repel one another, causing the ring to leap.
- When the switch is closed and the battery terminals are reversed, the magnetic field is reversed as well because the direction of the current is likewise reversed.
- The two laws that assist us in understanding this phenomenon are Faraday's laws and Lenz's law of electromagnetic induction.
When the induced current is applied in the same direction as the coil, the motion is countered by Lenz's law. The magnet in the loop exerts force to generate the current. To counteract the change, the magnet's current must impose a force on it.
"Whenever a conductor is placed in a varying magnetic field, an electromotive force is induced," asserts Faraday's first law of electromagnetic induction. Similarly, when the conductor circuit is closed, a current is induced, which is referred to as induced current."
APPEARS IN
संबंधित प्रश्न
State Ampere’s circuital law.
In Ampere's \[\oint \vec{B} \cdot d \vec{l} = \mu_0 i,\] the current outside the curve is not included on the right hand side. Does it mean that the magnetic field B calculated by using Ampere's law, gives the contribution of only the currents crossing the area bounded by the curve?
A thin but long, hollow, cylindrical tube of radius r carries i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
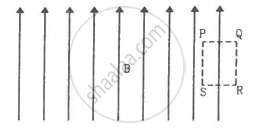
Sometimes we show an idealised magnetic field which is uniform in a given region and falls to zero abruptly. One such field is represented in figure. Using Ampere's law over the path PQRS, show that such a field is not possible.
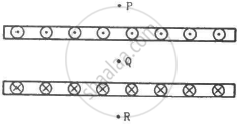
Two large metal sheets carry currents as shown in figure. The current through a strip of width dl is Kdl where K is a constant. Find the magnetic field at the points P, Q and R.
Define ampere.
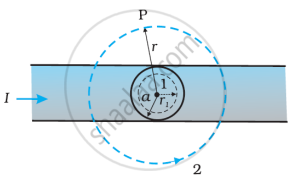
The given figure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. Calculate the magnetic field in the region r < a and r > a.
Briefly explain various ways to increase the strength of the magnetic field produced by a given solenoid.
Using Ampere’s circuital law, obtain an expression for magnetic flux density ‘B’ at a point near an infinitely long and straight conductor, carrying a current I.
