Advertisements
Advertisements
प्रश्न
Select the correct option from the given alternatives:
A line passes through (2, 2) and is perpendicular to the line 3x + y = 3. Its y−interecpt is
पर्याय
`1/3`
`2/3`
1
`4/3`
उत्तर
`4/3`
Explanation:
Slope of line 3x + y = 3 is −3
∴ Slope of the line perpendicular to given line = `1/3`.
Equation of required line passing through (2, 2) and having slope `1/3` is
y − 2 = `1/3("x"-2)`
∴ 3y − 6 = x − 2
∴ x − 3y + 4 = 0
y-intercept = `(-4)/(-3)=4/3`
APPEARS IN
संबंधित प्रश्न
Find the slope of the following line which passes through the points:
E(2, 3), F(2, −1)
A line makes intercepts 3 and 3 on the co-ordinate axes. Find the inclination of the line.
Find the value of k for which points P(k, −1), Q(2, 1) and R(4, 5) are collinear.
A line passes through points A(x1, y1) and B(h, k). If the slope of the line is m then show that k − y1 = m(h − x1)
If points A(h, 0), B(0, k) and C(a, b) lie on a line then show that `"a"/"h" + "b"/"k"` = 1
Select the correct option from the given alternatives:
If kx + 2y − 1 = 0 and 6x − 4y + 2 = 0 are identical lines, then determine k
Answer the following question:
Find the value of k if the slope of the line passing through the points P(3, 4), Q(5, k) is 9
Answer the following question:
Find the value of k the points A(1, 3), B(4, 1), C(3, k) are collinear
Answer the following question:
Line through A(h, 3) and B(4, 1) intersect the line 7x − 9y − 19 = 0 at right angle Find the value of h
Find the equation of the lines passing through the point (1,1) with slope 3
If P(r, c) is midpoint of a line segment between the axes then show that `x/"r" + y/"c"` = 2
If p is length of perpendicular from origin to the line whose intercepts on the axes are a and b, then show that `1/("p"^3) = 1/("a"^2) + 1/("b"^2)`
An object was launched from a place P in constant speed to hit a target. At the 15th second, it was 1400 m from the target, and at the 18th second 800 m away. Find the distance between the place and the target
An object was launched from a place P in constant speed to hit a target. At the 15th second, it was 1400 m from the target, and at the 18th second 800 m away. Find the distance covered by it in 15 seconds
Find the equation of the line, if the perpendicular drawn from the origin makes an angle 30° with x-axis and its length is 12
Show that the points (1, 3), (2, 1) and `(1/2, 4)` are collinear, by using concept of slope
Show that the points (1, 3), (2, 1) and `(1/2, 4)` are collinear, by using a straight line
Show that the points (1, 3), (2, 1) and `(1/2, 4)` are collinear, by using any other method
A 150 m long train is moving with constant velocity of 12.5 m/s. Find the equation of the motion of the train
A spring was hung from a hook in the ceiling. A number of different weights were attached to the spring to make it stretch, and the total length of the spring was measured each time is shown in the following table
| Weight (kg) | 2 | 4 | 5 | 8 |
| Length (cm) | 3 | 4 | 4.5 | 6 |
How long will the spring be when 6 kilograms of weight on it?
A family is using Liquefied petroleum gas (LPG) of weight 14.2 kg for consumption. (Full weight 29.5kg includes the empty cylinders tare weight of 15.3kg.). If it is used with constant rate then it lasts for 24 days. Then the new cylinder is replaced. Find the equation relating the quantity of gas in the cylinder to the days
A family is using Liquefied petroleum gas (LPG) of weight 14.2 kg for consumption. (Full weight 29.5kg includes the empty cylinders tare weight of 15.3kg.). If it is used with constant rate then it lasts for 24 days. Then the new cylinder is replaced. Draw the graph for first 96days
In a shopping mall there is a hall of cuboid shape with dimension 800 × 800 × 720 units, which needs to be added the facility of an escalator in the path as shown by the dotted line in the figure. Find the heights at which the escalator changes its direction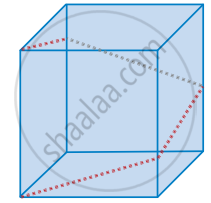
The distance of the origin from the centroid of the triangle whose two sides have the equations. x – 2y + 1 = 0 and 2x – y – 1 = 0 and whose orthocenter is `(7/3. 7/3)` is ______.
A point on the straight line, 3x + 5y = 15 which is equidistant from the coordinate, axes will lie only in ______.
The number of possible tangents which can be drawn to the curve 4x2 – 9y2 = 36, which are perpendicular to the straight line 5x + 2y – 10 = 0 is ______.
The equation of the line passing through the point (–3, 1) and bisecting the angle between co-ordinate axes is ______.
