Advertisements
Advertisements
प्रश्न
Show that the vector area of a triangle ABC, the position vectors of whose vertices are `bar"a", bar"b" and bar"c"` is `1/2[bar"a" xx bar"b" + bar"b" xx bar"c" + bar"c" xx bar"a"]`.
उत्तर
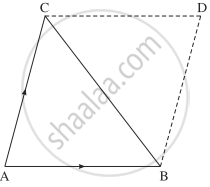
Consider the triangle ABC.
Complete the parallelogram ABDC.
Vector area of Δ ABC.
`= 1/2("vector area of parallelogram ABDC")`
`= 1/2(bar"AB" xx bar"AC")`
`= 1/2[(bar"b" - bar"a")xx(bar"c" - bar"a")] ......[∵ bar"AB" = bar"b" - bar"a" and bar"AC" = bar"c" - bar"a"]`
`= 1/2 [bar"b" xx bar"c" - bar"b" xx bar"a" - bar"a" xx bar"c" + bar"a" xx bar"a"]`
`= 1/2 [bar"b"xxbar"c" + bar"a"xxbar"b" + bar"c"xx bar"a" + bar0]`
`= 1/2[bar"a"xxbar"b" + bar"b" xx bar"c" + bar"c" xx bar"a"]`
APPEARS IN
संबंधित प्रश्न
If \[\overrightarrow{a} = \hat{i} + \hat{j} , \overrightarrow{b} = \hat{j} + \hat{k} , \overrightarrow{c} = \hat{k} + \hat{i}\], find the unit vector in the direction of \[\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}\].
Write a unit vector in the direction of \[\overrightarrow{b} = 2 \hat{i} + \hat{j} + 2 \hat{k}\].
For what value of 'a' the vectors \[2 \hat{i} - 3 \hat{j} + 4 \hat{k} \text{ and }a \hat{i} + 6 \hat{j} - 8 \hat{k}\] are collinear?
In a triangle OAC, if B is the mid-point of side AC and \[\overrightarrow{OA} = \overrightarrow{a} , \overrightarrow{OB} = \overrightarrow{b}\], then what is \[\overrightarrow{OC}\].
If \[\vec{a} , \vec{b}\] are the vectors forming consecutive sides of a regular hexagon ABCDEF, then the vector representing side CD is
Forces 3 O \[\vec{A}\], 5 O \[\vec{B}\] act along OA and OB. If their resultant passes through C on AB, then
If \[\vec{a}\], \[\vec{b}\], \[\vec{c}\] and \[\vec{d}\] are the position vectors of points A, B, C, D such that no three of them are collinear and \[\vec{a} + \vec{c} = \vec{b} + \vec{d} ,\] then ABCD is a
Find the vector equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0. Hence find whether the plane thus obtained contains the line \[\frac{x + 2}{5} = \frac{y - 3}{4} = \frac{z}{5}\] or not.
If `veca` and `vecb` are non- collinear vectors, find the value of x such that the vectors `barα = (x - 2)veca + vecb` and `barβ = (3+2x)bara - 2barb` are collinear.
Find the coordinates of the point which is located three units behind the YZ-plane, four units to the right of XZ-plane, and five units above the XY-plane.
Find the area of the traingle with vertices (1, 1, 0), (1, 0, 1) and (0, 1, 1).
Select the correct option from the given alternatives:
The volume of tetrahedron whose vectices are (1,-6,10), (-1, -3, 7), (5, -1, λ) and (7, -4, 7) is 11 cu units, then the value of λ is
Select the correct option from the given alternatives:
If `bar"a" "and" bar"b"` are unit vectors, then what is the angle between `bar"a"` and `bar"b"` for `sqrt3bar"a" - bar"b"` to be a unit vector?
If P is orthocentre, Q is the circumcentre and G is the centroid of a triangle ABC, then prove that `bar"QP" = 3bar"QG"`.
Express `hat"i" + 4hat"j" - 4hat"k"` as the linear combination of the vectors `2hat"i" - hat"j" + 3hat"k", hat"i" - 2hat"j" + 4hat"k"` and `- hat"i" + 3hat"j" - 5hat"k"`.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a" xx(bar"b" xx bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a".(bar"b" + bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`|bar"a"|. (bar"b" + bar"c")`
The vector eqliation of line 2x - 2 = 3y + 1 = 6z - 2 is
If the vectors `xhat"i" - 3hat"j" + 7hat"k" and hat"i" + "y"hat"j" - "z"hat"k"` are collinear then the value of `"xy"^2/"z"` is equal.
For any non zero vector, a, b, c a · ((b + c) × (a + b + c)] = ______.
If the vectors `overlinea = 2hati - qhatj + 3hatk` and `overlineb = 4hati - 5hatj + 6hatk` are collinear, then the value of q is ______
For 0 < θ < π, if A = `[(costheta, -sintheta), (sintheta, costheta)]`, then ______
Find a vector of magnitude 11 in the direction opposite to that of `vec"PQ"` where P and Q are the points (1, 3, 2) and (–1, 0, 8), respectively.
The vector with initial point P (2, –3, 5) and terminal point Q(3, –4, 7) is ______.
If `veca` and `vecb` are unit vectors, then what is the angle between `veca` and `vecb` for `sqrt(3) veca - vecb` to be a unit vector?
Find a unit vector in the direction of `vec"PQ"`, where P and Q have co-ordinates (5, 0, 8) and (3, 3, 2), respectively
Using vectors, find the value of k such that the points (k, – 10, 3), (1, –1, 3) and (3, 5, 3) are collinear.
If `vec"a"` and `vec"b"` are adjacent sides of a rhombus, then `vec"a" * vec"b"` = 0
The unit vector perpendicular to the vectors `6hati + 2hatj + 3hatk` and `3hati - 6hatj - 2hatk` is
If `veca` and `vecb` are two collinear vectors then which of the following are incorrect.
Find `|vecx|`, if for a unit vector `veca, (vecx - veca) * (vecx + veca)` = 12
In the triangle PQR, `bar(PQ) = 2bara` and `bar(QR)=2barb`. The mid-point of PR is M. Find following vectors in terms of `bar a and bar b `.
- `bar("PR")`
- `bar("PM")`
- `bar("QM")`
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk` and `3hati + 4hatk` form a triangle or not.
Check whether the vectors `2hati +2hatj+3hatk, -3hati +3hatj +2hatk and 3hati +4hatk` form a triangle or not.
In the triangle PQR, `bar(PQ)` = 2`bara` and `bar(QR)` = 2`barb`. The mid-point of PR is M. Find following vectors in terms of `bara` and `barb`.
- `bar(PR)`
- `bar(PM)`
- `bar(QM)`
Check whether the vectors `2hati + 2hatj +3hatk, - 3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
