Advertisements
Advertisements
प्रश्न
संलग्न आकृति में वृत्त का केंद्र P और रेख AB वृत्त की जीवा है। PA = 8 सेमी और जीवा AB वृत्त के केंद्र से 4 सेमी की दूरी पर हो तो रेखांकित भाग का क्षेत्रफल ज्ञात कीजिए। `(pi = 3.14, sqrt3 = 1.73)`
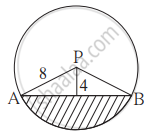
उत्तर
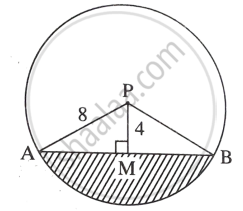
मानो कि, PM यह केंद्र से जीवा के बीच की दुरी है |
∴ PM = 4 सेमी
मानो, ∠APM = θ.
समकोण ΔPMA में,
cos θ = `"PM"/"PA"`
∴ cos θ = `4/8`
∴ cos θ = `1/2`
हम जानते है कि, cos 60° = `1/2`
∴ θ = 60°
∴ ∠APM = θ = 60°
इसी प्रकार, ∠BPM = 60°
∠APB = ∠APM + ∠BPM ..........(कोणों का योग गुणधर्म)
∴ ∠APB = 60° + 60°
∴ ∠APB = 120°
रेखांकित भाग यह वृत्तखंड AB है |
वृत्त की त्रिज्या (r) = 8 सेमी
m(चाप AB) = ∠APB = θ1 = 120°
द्वैत्रिज्य P-AB का क्षेत्रफल = `theta_1/360 xx pir^2`
= `120/360 xx 3.14 xx 8 xx 8`
= 66.986 सेमी2
≈ 66.99 सेमी2
समकोण ΔPMA में,
tan 60° = `"AM"/"PM"` .......(परिभाषा से)
∴ `sqrt3 = "AM"/4`
∴ AM = `4sqrt3` सेमी
रेख PM ⊥ जीवा AB
∴ AM = `1/2`AB .......(केंद्र से जीवा पर डाला गया लंब जीवा को समद्विभाजित करता है |)
∴ `4sqrt3 = 1/2`AB
∴ AB = `2 xx 4sqrt3`
∴ AB = `8sqrt3` सेमी
A(ΔPAB) = `1/2` × AB × PM
A(ΔPAB) = `1/2 xx 8sqrt3 xx 4`
∴ A(ΔPAB) = `16sqrt3`
∴ A(ΔPAB) = 16 × 1.73 .......`(sqrt3 = 1.73)`
∴ A(ΔPAB) = 27.68 सेमी2
A(वृत्तखंड AB) = A(द्वैत्रिज्य P-AB) - A(ΔPAB)
∴ A(वृत्तखंड AB) = 66.99 - 27.68
∴ A(वृत्तखंड AB) = 39.31 सेमी2
रेखांकित भाग का क्षेत्रफल 39.31 सेमी2 है |
APPEARS IN
संबंधित प्रश्न
O और P केंद्रवाले वृत्त परस्पर बिंदु A पर अंत:स्पर्श करते हैं, यदि BQ = 9, DE = 5, हो तो वृत्त की त्रिज्या ज्ञात करने के लिए नीचे दी गई कृति पूर्ण कीजिए।
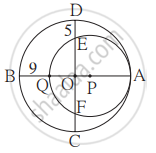
हल : माना बडे़ वृत्त की त्रिज्या = R
तथा छोटे वृत्त की त्रिज्या = r
OA, OB, OC और OD यह बड़े वृत्त की त्रिज्याएँ हैं।
∴ OA = OB = OC = OD = R
PQ = PA = r
OQ = OB - BQ = `square`
OE = OD - DE = `square`
P केंद्रवाले वृत्त में दो जीवाओं के अंत: प्रतिच्छेदन के गुणधर्मानुसार
OQ × OA = OE × OF
`square xx "R" = square xx square` ...............(∵ OE = OF)
R2 - 9R = R2 - 10R + 25
R = `square`
AQ = 2r = AB - BQ
2r = 50 - 9 = 41
r = `square` = `square`
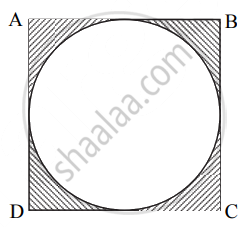
ऊपर दी गयी आकृति में `square`ABCD एक वर्ग है और एक वृत उसमें अंतर्लिखित है। वर्ग की सभी भुजायें वृत्त को स्पर्श करती हैं।
यदि AB = 14 सेमी, तो रेखांकित भाग का क्षेत्रफल ज्ञात कीजिए।
हल:
वर्ग का क्षेत्रफल = `(square)^2` ...(सूत्र)
= 142
= `square` वर्ग सेमी
∴ वृत्त का क्षेत्रफल = `square` ...(सूत्र)
= `22/7 xx 7 xx 7`
= 154 वर्ग सेमी
∴ रेखांकित भाग का क्षेत्रफल = (वर्ग का क्षेत्रफल) - (वृत्त का क्षेत्रफल)
= 196 - 154
= `square` वर्ग सेमी
