Balbharati solutions for Geometry (Mathematics 2) [Hindi] 10 Standard SSC Maharashtra State Board chapter 7 - महत्वमापन [Latest edition]

किसी शंकु के आधार की त्रिज्या 1.5 सेमी तथा लंब ऊँचाई 5 सेमी हो तो शंकु का घनफल ज्ञात कीजिए।

6 सेमी व्यासवाले गोले का घनफल ज्ञात कीजिए। 

किसी लंब वृत्ताकार बेलन के आधार की त्रिज्या 5 सेमी तथा ऊँचाई क्रमश: 40 सेमी हो तो उसका संपूर्ण पृष्ठफल ज्ञात कीजिए |

किसी गोले की त्रिज्या 7 सेमी हो तो उसका पृष्ठफल ज्ञात कीजिए।

किसी धातु के आयताकार बेलन (घनाभ) की लंबाई, चौड़ाई और ऊँचाई 44 सेमी, 21 सेमी और 12 सेमी है। उसे पिघलाकर 24 सेमी ऊँचाई का शंकु बनाया गया तो शंकु के आधार की त्रिज्या ज्ञात कीजिए। 

आकृति में निरीक्षण द्‌वारा ज्ञात कीजिए कि वृत्ताकार बेलन के आकार वाले बर्तन में कितना जग पानी भरा जाएगा?

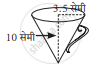
शंक्वाकार पानी का जग

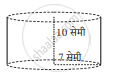
वृत्ताकार बेलन के आकार का पात्र 

किसी वृत्ताकार बेलन तथा शंकु का आधार समान है। वृत्ताकार बेलन पर शंकु को रखें वृत्ताकार बेलन की ऊँचाई 3 सेमी तथा उसके आधार का क्षेत्रफल 100 वर्ग सेमी है यदि संपूर्ण घनाकृति का घनफल 500 घसेमी हो तो संपूर्ण घनाकृति की ऊँचाई ज्ञात कीजिए।

संलग्न आकृति में दी गई जानकारी के आधार पर अर्धगोले, वृत्ताकार बेलन तथा शंकु से बनाए गए खिलौने का संपूर्ण पृष्ठफल ज्ञात कीजिए।

आकृति में वृत्ताकार बेलन के आकार की चपटी गोली का 10 सेमी लंबाई का एक वेष्टन है। एक गोली की त्रिज्या 7 मिमी और ऊँचाई 5 मिमी हो तो ऐसी कितनी गोलियाँ उस वेष्टन में समाविष्ट होंगी?

आकृति में बच्चों का एक खिलौना दर्शाया गया है। खिलौना एक अर्धगोले तथा शंकु की सहायता से बनाया गया है। आकृति में दर्शाए गए माप के आधारपर खिलौने का घनफल तथा पृष्ठफल ज्ञात कीजिए। (π = 3.14)

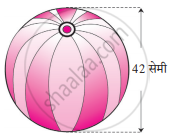
आकृति मे दर्शाए नुसार बीच बॉल का पृष्ठफल तथा घनफल ज्ञात कीजिए।

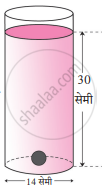
आकृति में दर्शाएनुसार लंब वृत्ताकार बेलनवाले ग्लास में पानी किनारे तक लबलबा भरा है | उसमें 2 सेमी व्यासवाले धातु की एक गोली डुबाने पर ग्लास में बचा शेष पानी का घनफल ज्ञात करो |  

30 सेमी ऊँचाई वाले शंकुछेद के आकार वाली बाल्टी के वृत्ताकार भागों की त्रिज्या 14 सेमी तथा 7 सेमी है उस बाल्टी में कितने लीटर पानी भरा जा सकता है? ज्ञात कीजिए। (1 लीटर = 1000 घसेमी)

शंकुछेद के वृत्ताकार भाग की त्रिज्या क्रमश: 14 सेमी तथा 6 सेमी तथा उसकी ऊँचाई 6 सेमी हो तो निम्नलिखित के मान ज्ञात कीजिए। (π = 3.14)

(1) शंकुछेद का वक्रपृष्ठफल

(2) शंकुछेद का संपूर्ण पृष्ठफल

(3) शंकुछेद का घनफल

किसी शंकुछेद के वृत्ताकार आधार की परिधि क्रमश: 132 सेमी तथा 88 सेमी तथा ऊँचाई 24 सेमी है। तो उस शंकुछेद का वक्रपृष्ठफल ज्ञात करने के लिए निम्नलिखित कृति पूर्ण कीजिए। `(pi = 22/7)`

परिधि₁ = 2πr₁ = 132

r₁ = `132/(2pi) = square` सेमी

परिधि₂ = 2πr₂ = 88

r₂ = `88/(2pi) = square` सेमी

शंकुछेद की तिरछी ऊँचाई = l

तथा l = `sqrt(h^2 + (r_1 - r_2)^2)`

∴ l = `sqrt(square^2 + square^2)`

l = `square` सेमी

शंकुछेद का वक्रपृष्ठफल = π(r₁ + r₂)l

= `pi xx square xx square`

= `square` वर्ग सेमी

किसी वृत्त की त्रिज्या 10 सेमी तथा वृत्त चाप का माप 54° हो तो उस चाप द्वारा सीमित द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए। (π =3.14)

किसी वृत्तचाप का माप 80° और त्रिज्या 18 सेमी है तो उसके वृत्तचाप की लंबाई ज्ञात कीजिए।(π =3.14) 

किसी द्वैत्रिज्य की त्रिज्या 3.5 सेमी तथा उसके वृत्त चाप की लंबाई 2.2 सेमी हो तो द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए।

किसी वृत्त की त्रिज्या 10 सेमी तथा उसके लघु द्वैत्रिज्य का क्षेत्रफल 100 वर्ग सेमी हो तो उसके दीर्घ द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए। (π = 3.14) 

15 सेमी त्रिज्यावाले किसी द्वैत्रिज्य का क्षेत्रफल 30 वर्ग सेमी हो तो संगत वृत्त चाप की लंबाई ज्ञात कीजिए। 

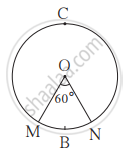
संलग्न आकृति में वृत्त की त्रिज्या 7 सेमी है और m(चाप MBN) = 60° तो

(1) वृत्त का क्षेत्रफल ज्ञात कीजिए।

(2) A(O - MBN) ज्ञात कीजिए।

(3) A(O - MCN) ज्ञात कीजिए।

संलग्न आकृति में, 3.4 सेमी त्रिज्यावाले द्वैत्रिज्य P-ABC की परिमिति 12.8 सेमी है तो द्वैत्रिज्य P-ABC का क्षेत्रफल ज्ञात कीजिए। 

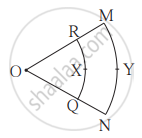
संलग्न आकृति में बिंदु O यह द्वैत्रिज्य का केंद्र है। ∠ROQ = ∠MON = 60°, OR = 7 सेमी, OM = 21 सेमी हो तो चाप RXQ तथा चाप MYN की लंबाई ज्ञात कीजिए। `(π = 22/7)` 

संलग्न आकृति में A(P-ABC) = 154 वर्ग सेमी और वृत्त की त्रिज्या 14 सेमी हो, तो

(1) ∠APC का माप ज्ञात कीजिए।

(2) चाप ABC की लंबाई ज्ञात कीजिए।

किसी द्‌वैत्रिज्य की त्रिज्या 7 सेमी है। यदि द्वैत्रिज्य के चाप का माप निम्नलिखित है तो द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए। 

30°

किसी द्‌वैत्रिज्य की त्रिज्या 7 सेमी है। यदि द्वैत्रिज्य के चाप का माप निम्नलिखित है तो द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए। 

210°

किसी द्‌वैत्रिज्य की त्रिज्या 7 सेमी है। यदि द्वैत्रिज्य के चाप का माप निम्नलिखित है तो द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए। 

3 समकोण

लघु द्वैत्रिज्य का क्षेत्रफल 3.85 वर्ग सेमी तथा उसके संगत केंद्रीय कोण का माप 36° हो तो उस वृत्त की त्रिज्या ज्ञात कीजिए। 

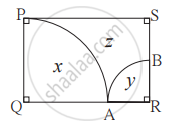
संलग्न आकृति में `square`PQRS एक आयत है। PQ = 14 सेमी, QR = 21 सेमी, हो तो आकृति में दर्शाएनुसार x, y और z इस प्रत्येक भाग का क्षेत्रफल ज्ञात कीजिए।

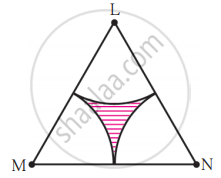
ΔLMN समबाहु त्रिभुज है। LM = 14 सेमी. त्रिभुज के प्रत्येक शीर्ष बिंदु को केंद्र मानकर तथा 7 सेमी त्रिज्या लेकर आकृति में दर्शाएनुसार तीन द्वैत्रिज्य खींचकर उसके आधार पर,

(1) A (ΔLMN) = ? 

(2) एक द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए।

(3) तीनों द्वैत्रिज्यों का संपूर्ण क्षेत्रफल ज्ञात कीजिए।

(4) रेखांकित भाग का क्षेत्रफल ज्ञात कीजिए।

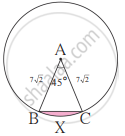
आकृति में बिंदु A केंद्रवाले वृत्त में ∠ABC = 45°, AC = `7sqrt2` सेमी, हो तो वृत्तखंड BXC का क्षेत्रफल ज्ञात कीजिए। (π = 3.14, `sqrt2` = 1.41)

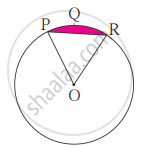
आकृति में बिंदु O वृत्त का केंद्र है। m(चाप PQR) = 60°, OP = 10 सेमी, हो तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। (π = 3.14, `sqrt3` = 1.73)

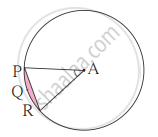
संलग्न आकृति में A केंद्र वाले वृत्त में ∠PAR = 30° AP = 7.5 हो तो, वृत्तखंड PQR का क्षेत्रफल ज्ञात कीजिए। (π = 3.14) 

आकृति में O केंद्रवाले किसी वृत्त में PQ जीवा है। ∠POQ = 90°, और छायांकित भाग का क्षेत्रफल 114 वसेमी हो तो वृत्त कि त्रिज्या ज्ञात कीजिए। (π = 3.14) 

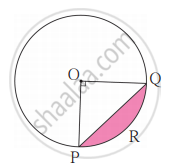
15 सेमी त्रिज्यावाले किसी वृत्त में जीवा PQ वृत्त के केंद्र से 60° का कोण बनाती है। उस जीवा से बनने वाले दीर्घ वृत्तखंड और लघु वृत्तखंड का क्षेत्रफल ज्ञात कीजिए। (π = 3.14, `sqrt3` = 1.73)

नीचे दिए गए बहुवैकल्पिक प्रश्न में से उचित विकल्प चुनकर लिखिए।

किसी वृत्त की परिधि तथा क्षेत्रफल का अनुपात 2ः7 हो तो उस वृत्त की परिधि कितनी होगी?

नीचे दिए गए बहुवैकल्पिक प्रश्न में से उचित विकल्प चुनकर लिखिए।

44 सेमी लंबाईवाले किसी वृत्त चाप का माप 160° हो तो उस वृत्त की परिधि कितनी होगी? 

नीचे दिए गए बहुवैकल्पिक प्रश्न में से उचित विकल्प चुनकर लिखिए।

किसी चाप का माप 90° तथा त्रिज्या 7 सेमी हो तो द्वैत्रिज्य की परिमिति ज्ञात कीजिए। 

नीचे दिए गए बहुवैकल्पिक प्रश्न में से उचित विकल्प चुनकर लिखिए।

किसी शंकु के आधार की त्रिज्या 7 सेमी तथा ऊँचाई 24 सेमी हो तो शंकु का वक्रपृष्ठफल कितना होगा?

नीचे दिए गए बहुवैकल्पिक प्रश्न में से उचित विकल्प चुनकर लिखिए।

5 सेमी त्रिज्या वाले किसी लंबवृत्ताकार बेलन का वक्रपृष्ठफल 440 सेमी² हो तो उस लंबवृत्ताकार बेलन की ऊँचाई कितनी होगी? 

नीचे दिए गए बहुवैकल्पिक प्रश्न में से उचित विकल्प चुनकर लिखिए।

किसी शंकु को पिघलाकर उसके आधार की त्रिज्या के बराबर त्रिज्या वाला लंबवृत्ताकार बेलन बनाया गया। यदि लंबवृत्ताकार बेलन की ऊँचाई 5 सेमी हो तो शंकु की ऊँचाई कितनी होगी?

नीचे दिए गए बहुवैकल्पिक प्रश्न में से उचित विकल्प चुनकर लिखिए।

0.01 सेमी भुजावाले समघन का घनफल कितना घसेमी होगा?

नीचे दिए गए बहुवैकल्पिक प्रश्न में से उचित विकल्प चुनकर लिखिए।

एक घन मीटर घनफल वाले समघन के भुजा की लंबाई कितनी होगी?

किसी शंकु छेद के आकारवाले कपड़े धोने के टब की ऊँचाई 21 सेमी है। टब के दोनों वृत्ताकार भाग की त्रिज्या क्रमश: 20 सेमी तथा 15 सेमी है। उस टब में पानी रखने की क्षमता कितनी होगी? `(pi = 22/7)`

1 सेमी त्रिज्यावाले प्लास्टिक की छोटी गोली पिघलाकर लंबवृत्ताकार बेलन के आकार की नली बनाई गई। नली की मोटाई 2 सेमी, ऊँचाई 90 सेमी तथा बाहरी त्रिज्या 30 सेमी हो तो नली बनवाने के लिए कितनी गोलियाँ पिघलानी पड़ेगी? 

16 सेमी लंबाई, 11 सेमी चौड़ाई, 10 सेमी ऊँचाईवाले किसी धातु के आयताकार बेलन (घनाभ) से धातु के 2 मिमी मोटे तथा 2 सेमी व्यासवाले कुछ सिक्के बनाने हों तो ऐसे कितने सिक्के बनेंगे ज्ञात कीजिए? 

किसी मैदान को समतल करने के लिए 120 सेमी व्यास तथा 84 सेमी लंबाई वाले रोलर के 200 फेरे लगते हैं, तो 10 रु प्रतिवर्ग मीटर की दर से मैदान समतल करने में कितना खर्च लगेगा?

किसी धातु के खोखले गोले का व्यास 12 सेमी तथा उसकी मोटाई 0.01 मीटर हो तब उस खोखले गोले के बाहरी भाग का पृष्ठफल ज्ञात कीजिए तथा धातु का घनत्व 8.88 ग्राम प्रति घन सेमी हो तो उस खोखले गोले का द्रव्यमान ज्ञात कीजिए।

किसी वृत्ताकार बेलन के आकार वाली बाल्टी के आधार का व्यास 28 सेमी तथा ऊँचाई 20 सेमी है बाल्टी रेत से पूर्णत: भरी है उस बाल्टी की रेत को जमीन पर इसतरह पलटिए कि रेत का शंकु बने। रेत के शंकु की ऊँचाई 14 सेमी हो तो शंकु के आधार का क्षेत्रफल ज्ञात कीजिए।

9 सेमी त्रिज्यावाले किसी धातु के ठोस गोले को पिघलाकर 4 मिमी व्यासवाला धातु का तार बनाया जाय तो उस तार की लंबाई कितने मीटर होगी? 

6 सेमी त्रिज्यावाले किसी वृत्त के एक द्वैत्रिज्य का क्षेत्रफल 15π सेमी² हो तो उस द्वैत्रिज्य के चाप का माप तथा वृत्त चाप की लंबाई ज्ञात कीजिए। 

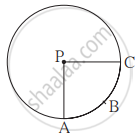
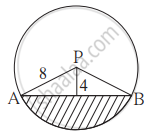
संलग्न आकृति में वृत्त का केंद्र P और रेख AB वृत्त की जीवा है। PA = 8 सेमी और जीवा AB वृत्त के केंद्र से 4 सेमी की दूरी पर हो तो रेखांकित भाग का क्षेत्रफल ज्ञात कीजिए। `(pi = 3.14, sqrt3 = 1.73)`

द्वैत्रिज्य A-PCQ में `square`ABCD यह एक वर्ग है। द्वैत्रिज्य C - BXD की त्रिज्या 20 सेमी हो तो छायांकित भाग का क्षेत्रफल ज्ञात करने के लिए नीचे दी गई कृति पूर्ण कीजिए।

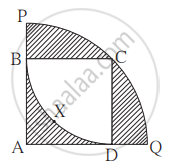
हल : वर्ग ABCD की भुजा = द्वैत्रिज्य C - BXD की त्रिज्या = `square` सेमी 

वर्ग का क्षेत्रफल = (भुजा)² = `square^2 = square` ............(I)

वर्ग के छायांकित भाग का क्षेत्रफल 

= वर्ग ABCD का क्षेत्रफल - द्वैत्रिज्य C - BXD का क्षेत्रफल

= `square - theta/360 xx pir^2`

= `square - 90/360 xx 3.14/1 xx 400/1`

= `square - 314`

= `square`

बड़े द्वैत्रिज्य की त्रिज्या = वर्ग ABCD के विकर्ण की लंबाई

= `20sqrt2`

बड़े द्वैत्रिज्य में वर्ग के बाहर के छायांकित भाग का क्षेत्रफल

= द्वैत्रिज्य (A - PCQ) का क्षेत्रफल - वर्ग ABCD का क्षेत्रफल

= A(A - PCQ) - A(`square` ABCD)

= `(theta/360 xx pi xx r^2) - square^2`

= `90/360 xx 3.14(20sqrt2)^2 - (20)^2`

= `square - square`

= `square`

∴ छायांकित भाग का संपूर्ण क्षेत्रफल = 86 + 228 = 314 वसेमी

O और P केंद्रवाले वृत्त परस्पर बिंदु A पर अंत:स्पर्श करते हैं, यदि BQ = 9, DE = 5, हो तो वृत्त की त्रिज्या ज्ञात करने के लिए नीचे दी गई कृति पूर्ण कीजिए। 

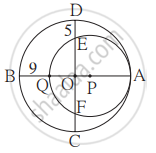
हल : माना बडे़ वृत्त की त्रिज्या = R 

तथा छोटे वृत्त की त्रिज्या = r

OA, OB, OC और OD यह बड़े वृत्त की त्रिज्याएँ हैं।

∴ OA = OB = OC = OD = R

PQ = PA = r

OQ = OB - BQ = `square`

OE = OD - DE = `square`

P केंद्रवाले वृत्त में दो जीवाओं के अंत: प्रतिच्छेदन के गुणधर्मानुसार

OQ × OA = OE × OF

`square xx "R" = square xx square` ...............(∵ OE = OF)

R² - 9R = R² - 10R + 25 

R = `square`

AQ = 2r = AB - BQ

2r = 50 - 9 = 41

r = `square` = `square`