Advertisements
Advertisements
प्रश्न
सोबतच्या आकृतीत, ∆ABC मध्ये, AD ⊥ BC, तर AB2 + CD2 = BD2 + AC2 हे सिद्ध करण्यासाठी खालील कृती पूर्ण करा.
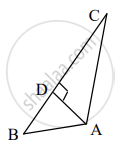
कृती: पायथागोरसच्या प्रमेयानुसार, काटकोन त्रिकोण ∆ADC मध्ये,
AC2 = AD2 + `square^2`
∴ AD2 = AC2 – CD2 …...........(i)
तसेच, पायथागोरसच्या प्रमेयानुसार, काटकोन त्रिकोण ∆ABD मध्ये,
AB2 = `square^2` + BD2
∴ AD2 = AB2 – BD2 …...… (ii)
∴ `square^2 - "BD"^2 = "AC"^2 - square^2` .....…….. (i) व (ii) वरून
∴ AB2 + CD2 = AC2 + BD2
उत्तर
पायथागोरसच्या प्रमेयानुसार, काटकोन त्रिकोण ∆ADC मध्ये,
AC2 = AD2 + CD2
∴ AD2 = AC2 – CD2 …...........(i)
तसेच, पायथागोरसच्या प्रमेयानुसार, काटकोन त्रिकोण ∆ABD मध्ये,
AB2 = AD2 + BD2
∴ AD2 = AB2 – BD2 …...… (ii)
∴ AB2 - "BD"^2 = AC2 - CD2 .....…….. (i) व (ii) वरून
∴ AB2 + CD2 = AC2 + BD2
APPEARS IN
संबंधित प्रश्न
एका चौरसाचा कर्ण 10 सेमी आहे तर त्याच्या बाजूची लांबी व परिमिती काढा.
आकृती मध्ये M हा बाजू QR चा मध्यबिंदू आहे. ∠PRQ = 90° असेल तर सिद्ध करा, PQ2 = 4PM2 - 3PR2
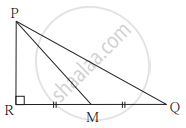
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
काटकोन त्रिकोणात काटकोन करणाऱ्या बाजूंच्या वर्गांची बेरीज 169 असेल, तर त्याच्या कर्णाची लांबी किती?
बाजूंच्या लांबी a, b, c असलेल्या त्रिकोणामध्ये जर a2 + b2 = c2 असेल तर तो कोणत्या प्रकारचा त्रिकोण असेल?
एका काटकोन त्रिकोणामध्ये काटकोन करणाऱ्या बाजू 9 सेमी व 12 सेमी आहेत, तर त्या त्रिकोणाच्या कर्णाची लांबी काढा.
आयताचे क्षेत्रफळ 192 चौसेमी असून त्याची लांबी 16 सेमी आहे, तर आयताच्या कर्णाची लांबी काढा.
ΔABC मध्ये रेख AD ⊥ रेख BC आणि DB = 3CD, तर सिद्ध करा : 2AB2 = 2AC2 + BC2
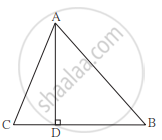
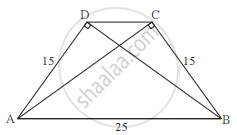
समलंब चौकोन ABCD मध्ये, रेख AB || रेख DC रेख BD ⊥ रेख AD, रेख AC ⊥ रेख BC, जर AD = 15, BC = 15 आणि AB = 25 असेल तर A(`square`ABCD) किती?
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका आयताची एक बाजू 12 आणि कर्णाची लांबी 20 असेल, तर त्या आयताच्या दुसऱ्या बाजूची लांबी किती?
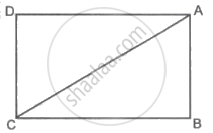
वरील आकृतीत `square`ABCD हा आयत आहे. जर AB = 5, AC = 13, तर बाजू BC ची लांबी काढण्यासाठी खालील कृती पर्ण करा.
कृती: ΔABC हा `square` त्रिकोण आहे.
∴ पायथागोरसच्या प्रमेयानुसार,
AB2 + BC2 = AC2
∴ 25 + BC2 = `square`
∴ BC2 = `square`
∴ BC = `square`
