Advertisements
Advertisements
प्रश्न
समलंब चौकोन ABCD मध्ये, रेख AB || रेख DC रेख BD ⊥ रेख AD, रेख AC ⊥ रेख BC, जर AD = 15, BC = 15 आणि AB = 25 असेल तर A(`square`ABCD) किती?
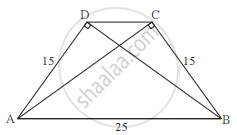
उत्तर
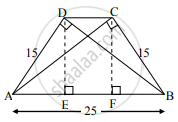
रचना: रेख DE ⊥ रेख AB, A-E-B आणि रेख CF ⊥ रेख AB, A-F-B काढा.
उकल:
ΔACB मध्ये, ∠ACB = 90° ....[पक्ष]
∴ AB2 = AC2 + BC2 ....[पायथागोरसचे प्रमेय]
∴ 252 = AC2 + 152
∴ AC2 = 625 – 225
= 400
∴ AC = `sqrt(400)` ....[दोन्ही बाजूंचे वर्गमूळ घेऊन]
= 20 एकक
आता, A(ΔABC) = `1/2 xx "BC" xx "AC"` ....(i)
तसेच, A(ΔABC) = `1/2 xx "AB" xx "CF"` ....(ii)
∴ `1/2 xx "BC" xx "AC"` = `1/2 xx "AB" xx "CF"` ...[(i) व (ii) वरून]
∴ BC × AC = AB × CF
∴ 15 × 20 = 25 × CF
∴ CF = `(15 xx 20)/25` = 12 एकक
ΔCFB मध्ये, ∠CFB = 90° ......[रचना]
∴ BC2 = CF2 + FB2 .....[पायथागोरसचे प्रमेय]
∴ 152 = 122 + FB2
∴ FB2 = 225 – 144
∴ FB2 = 81
∴ FB = `sqrt(81)` ....[दोन्ही बाजूंचे वर्गमूळ घेऊन]
= 9 एकक
त्याचप्रमाणे, आपण सिद्ध करू शकतो, की AE = 9 एकक
आता, AB = AE + EF + FB ...[A-E-F, E-F-B]
∴ 25 = 9 + EF + 9
∴ EF = 25 – 18 = 7 एकक
`square`CDEF मध्ये,
रेख EF || रेख DC ....[पक्ष, A-E-F, E-F-B]
रेख ED || रेख FC ....[एकाच रेषेवरील लंब रेषा एकमेकींना समांतर असतात.]
∴ `square`CDEF हा समांतरभुज चौकोन आहे.
∴ DC = EF = 7 एकक ....[समांतरभुज चौकोनाच्या समोरासमोरील बाजू]
समलंब चौकोनाचे क्षेत्रफळ = `1/2` × (समांतर बाजूंच्या × उंची लांबींची बेरीज)
A(`square`ABCD) = `1/2` × CF × (AB + CD)
= `1/2 xx 12 xx (25 + 7)`
= `1/2 xx 12 xx 32`
∴ A(`square`ABCD) = 192 चौ. एकक
APPEARS IN
संबंधित प्रश्न
एका आयताची लांबी 35 सेमी व रुंदी 12 सेमी आहे तर त्या आयताच्या कर्णाची लांबी काढा.
आयताच्या बाजू 11 सेमी व 60 सेमी असतील, तर त्याच्या कर्णाची लांबी काढा.
एका काटकोन त्रिकोणामध्ये काटकोन करणाऱ्या बाजू 9 सेमी व 12 सेमी आहेत, तर त्या त्रिकोणाच्या कर्णाची लांबी काढा.
ΔABC मध्ये ∠BAC = 90°, रेख BL व रेख CM या ΔABC च्या मध्यगा आहेत, तर सिद्ध करा : 4(BL2 + CM2 ) = 5BC2.
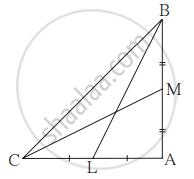
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका चौरसाच्या कर्णाची लांबी `sqrt2` सेमी असेल, तर त्या चौरसाच्या प्रत्येक बाजूची लांबी किती?
पुढील प्रत्येक उपप्रश्नासाठी 4 पर्यायी उत्तरे दिली आहेत. त्यांपैकी अचूक उत्तराचा योग्य पर्याय निवडून त्याचे वर्णाक्षर लिहा.
एका आयताची एक बाजू 12 आणि कर्णाची लांबी 20 असेल, तर त्या आयताच्या दुसऱ्या बाजूची लांबी किती?
एका काटकोन त्रिकोणामध्ये काटकोन करणाऱ्या बाजू 24 सेमी व 18 सेमी असतील, तर त्याच्या कर्णाची लांबी काढा.
10 मीटर लांबीची एक शिडी जमिनीपासून 8 मीटर उंचीच्या एका खिडकीपाशी पोहोचते, तर त्या भिंतीचा पाया व शिडीचे खालचे टोक यांमधील अंतर काढण्यासाठी खालील कृती पूर्ण करा.
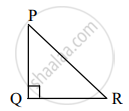
कृती: समजा, सोबतच्या आकृतीत,
PQ ही भिंतीची उंची आहे.
PR ही शिडी आहे आणि QR त्या भिंतीचा पाया व शिडीचे खालचे टोक यांमधील अंतर आहे.
∆PQR मध्ये, ∠PQR = 90°,
पायथागोरसच्या प्रमेयानुसार, PQ2 + `square` = PR2 … (i)
PR = 10, PQ = `square`
या किमती (i) मध्ये ठेवून,
QR2 + 82 = 102
QR2 = 102 – 82
QR2 = `square - 64`
QR2 = `square`
QR = 6
यावरून, त्या भिंतीचा पाया व शिडीचे खालचे टोक यांमधील अंतर 6 मीटर आहे.
काटकोन त्रिकोणात काटकोन करणाऱ्या बाजू 9 सेमी व 12 सेमी आहेत, तर त्या त्रिकोणाच्या कर्णाची लांबी माहीत करण्यासाठी कृती पूर्ण करा.
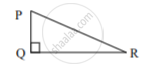
कृती: ∆PQR मध्ये, ∠PQR = 90°
पायथागोरसच्या प्रमेयानुसार,
PQ2 + `square` = PR2 .........…(i)
PR2 = 92 + 122
PR2 = `square + 144`
∴ PR2 = `square`
∴ PR = 15
त्रिकोणाचा कर्ण = `square`
समद्विभुज काटकोन त्रिकोणाच्या एकरूप बाजूंची लांबी 7 सेमी आहे. त्याची परिमिती काढा.
