Advertisements
Advertisements
प्रश्न
Solve for x
`(x - 1)/(2x + 1) + (2x + 1)/(x - 1) = 2, "where x" != -1/2, 1`
उत्तर
`(x - 1)/(2x + 1) + (2x + 1)/(x - 1) = 2`
`=>((x - 1)^2 + (2x + 1)^2)/((2x + 1)(x + 1)) = 2`
`=> (x^2 + 1 -2x + 4x^2 + 1 + 4x)/(2x^2 - 2x + x - 1) = 2`
`=> 5x^2 + 2x + 2 = 4x^2 - 2x - 2`
`=> x^2 + 4x + 4 = 0`
`=> (x + 2)^2 = 0`
⇒ x= -2 , -2
APPEARS IN
संबंधित प्रश्न
Divide 29 into two parts so that the sum of the squares of the parts is 425.
The sum of a numbers and its positive square root is 6/25. Find the numbers.
`x^2-6x+3=0`
Find the value of k for which the following equations have real and equal roots:
\[x^2 - 2\left( k + 1 \right)x + k^2 = 0\]
If the equation x2 − ax + 1 = 0 has two distinct roots, then
Solve the following equation: `x^2 + (a + 1/a)x + 1 = 0`
Solve the following quadratic equation by factorisation:
x2 - 3x - 10 = 0
Solve the following equation by factorization
`(x - 3)/(x + 3) + (x + 3)/(x - 3) = 2(1)/(2)`
Two natural numbers are in the ratio 3 : 4. Find the numbers if the difference between their squares is 175.
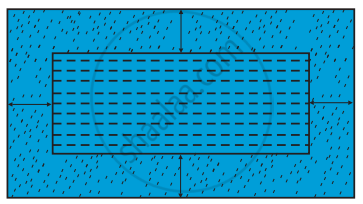
In the centre of a rectangular lawn of dimensions 50 m × 40 m, a rectangular pond has to be constructed so that the area of the grass surrounding the pond would be 1184 m2 [see figure]. Find the length and breadth of the pond.