Advertisements
Advertisements
प्रश्न
State with reason whether the following statement is ‘true’ or ‘false’.
Every parallelogram is a rhombus.
पर्याय
True
False
उत्तर
This statement is False.
Reason:
All the sides of a rhombus are congruent, while the opposite sides of a parallelogram are congruent.
APPEARS IN
संबंधित प्रश्न
Two opposite angles of a parallelogram are (3x − 2)° and (50 − x)°. Find the measure of each angle of the parallelogram.
Which of the following statement is true for a rhombus?
Two of its angles are at right angles
Fill in the blank, in each of the following, so as to make the statement true:
If the diagonals of a parallelogram bisect each other at right angles, then it is a ......
ABCD is a rhombus. If ∠ACB = 40°, find ∠ADB.
Construct a rhombus whose diagonals are of length 10 cm and 6 cm.
Draw a rhombus ABCD, if AB = 6 cm and AC = 5 cm.
Diagonals of a parallelogram intersect each other at point O. If AO = 5, BO = 12 and AB = 13 then show that `square`ABCD is a rhombus.
If opposite angles of a rhombus are (2x)° and (3x - 40)° then value of x is ______.
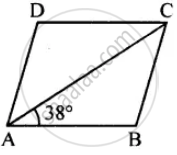
ABCD is a rhombus. If ∠BAC = 38°, find :
(i) ∠ACB
(ii) ∠DAC
(iii) ∠ADC.
A rhombus is a parallelogram in which ______ sides are equal.
