Advertisements
Advertisements
प्रश्न
The centre of a circle is (a+2, a-1). Find the value of a, given that the circle passes through the points (2, -2) and (8, -2).
उत्तर
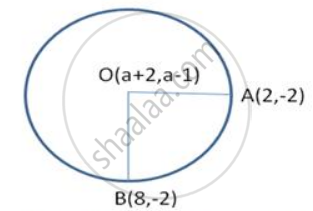
OA = OB [radii of same circle]
∴ OA2 = OB2
(a + 2 - 2)2 + (a - 1 + 2)2 = (a + 2 - 8)2 + (a - 1 + 2)2
a2 + (a + 1)2 = (a - 6)2 + (a + 1)2
a2 = a2 + 36 - 12a
12 a = 36
a = 3
APPEARS IN
संबंधित प्रश्न
Given a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D.
The mid-point of the line segment joining (2a, 4) and (–2, 2b) is (1, 2a + 1). Find the values of a and b.
Complete the table below the graph with the help of the following graph.

| Sr. No. | First point | Second point | Co-ordinates of first point (x1 , y1) | Co-ordinates of second point (x2 , y2) | `(y_2 - y_2)/(x_2 - x_2)` |
| 1 | C | E | (1, 0) | (3,4) | `4/2=2` |
| 2 | A | B | (-1,-4) | (0,-2) | `2/1 = 2` |
| 3 | B | D | (0,-2) | (2,2) | `4/2=2` |
If (-3, 2), (1, -2) and (5, 6) are the midpoints of the sides of a triangle, find the coordinates of the vertices of the triangle.
Find the length of the median through the vertex A of triangle ABC whose vertices are A (7, -3), B(S, 3) and C(3, -1).
Let A(-a, 0), B(0, a) and C(α , β) be the vertices of the L1 ABC and G be its centroid . Prove that
GA2 + GB2 + GC2 = `1/3` (AB2 + BC2 + CA2)
The centre ‘O’ of a circle has the coordinates (4, 5) and one point on the circumference is (8, 10). Find the coordinates of the other end of the diameter of the circle through this point.
The mid-point of the sides of a triangle are (2, 4), (−2, 3) and (5, 2). Find the coordinates of the vertices of the triangle
The coordinates of the point C dividing the line segment joining the points P(2, 4) and Q(5, 7) internally in the ratio 2 : 1 is
Find the coordinates of point P where P is the midpoint of a line segment AB with A(–4, 2) and B(6, 2).
Solution :

Suppose, (–4, 2) = (x1, y1) and (6, 2) = (x2, y2) and co-ordinates of P are (x, y).
∴ According to the midpoint theorem,
x = `(x_1 + x_2)/2 = (square + 6)/2 = square/2 = square`
y = `(y_1 + y_2)/2 = (2 + square)/2 = 4/2 = square`
∴ Co-ordinates of midpoint P are `square`.
