Advertisements
Advertisements
प्रश्न
The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC = 32º and ∠AOB = 70º, then ∠DBC is equal to ______.
पर्याय
24º
86º
38º
32º
उत्तर
The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC = 32º and ∠AOB = 70º, then ∠DBC is equal to 38º.
Explanation:
Given: ∠AOB = 70°
∠DAC = 32°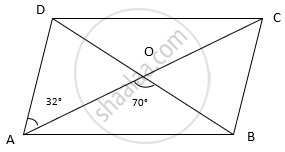
∵ AD || BC and AC is transversal
∴ ∠ACB = 32°
Now, ∠AOB + ∠BOC = 180°
⇒ 70° + ∠BOC = 180°
⇒ ∠BOC = 180° – 70°
⇒ ∠BOC = 110°
Sum of all angles of a triangle = 180°
⇒ ∠BOC + ∠BCO + ∠OBC = 180°
⇒ 110° + 32° + ∠OBC = 180°
⇒ 142° + ∠OBC = 180°
⇒ ∠OBC = 180° – 142°
⇒ ∠OBC = 38°
Hence, ∠DBC = 38°
APPEARS IN
संबंधित प्रश्न
Diagonals AC and BD of a parallelogram ABCD intersect each other at O. If OA = 3 cm and OD = 2 cm, determine the lengths of AC and BD.
E and F are points on diagonal AC of a parallelogram ABCD such that AE = CF. Show that BFDE is a parallelogram.
A diagonal of a parallelogram bisects one of its angles. Show that it is a rhombus.
In the following figure, AB || DE, AB = DE, AC || DF and AC = DF. Prove that BC || EF and BC = EF.

P and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.
ABCD is a rectangle in which diagonal BD bisects ∠B. Show that ABCD is a square.
P is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
If diagonals of a quadrilateral bisect each other, it must be a parallelogram.
The point of intersection of diagonals of a quadrilateral divides one diagonal in the ratio 1:2. Can it be a parallelogram? Why or why not?
Two sticks each of length 5 cm are crossing each other such that they bisect each other. What shape is formed by joining their endpoints? Give reason.
