Advertisements
Advertisements
प्रश्न
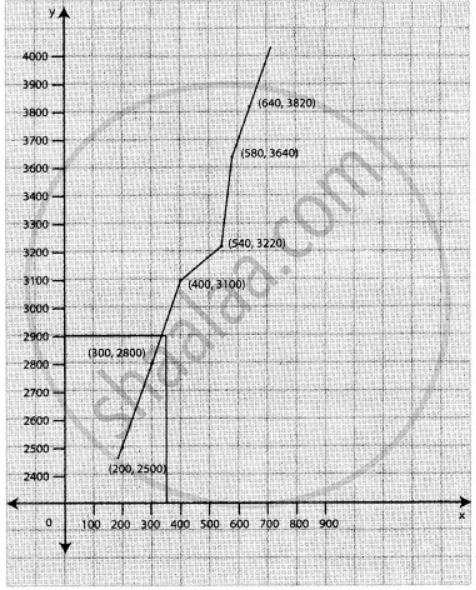
The following data relates to indirect labour expenses and the level of output
| Months | Jan | Feb | Mar |
| Units of output | 200 | 300 | 400 |
| Indirect labour expenses (Rs) |
2500 | 2800 | 3100 |
| Months | Apr | May | June |
| Units of output | 640 | 540 | 580 |
| Indirect labour expenses (Rs) |
3820 | 3220 | 3640 |
Estimate the expenses at a level of output of 350 units, by using graphic method.
उत्तर
APPEARS IN
संबंधित प्रश्न
The population of a city in a censes taken once in 10 years is given below. Estimate the population in the year 1955.
| Year | 1951 | 1961 | 1971 | 1981 |
| Population in lakhs |
35 | 42 | 58 | 84 |
In an examination the number of candidates who secured marks between certain intervals was as follows:
| Marks | 0 - 19 | 20 - 39 | 40 - 59 | 60 - 79 | 80 - 99 |
| No. of candidates |
41 | 62 | 65 | 50 | 17 |
Estimate the number of candidates whose marks are less than 70.
The following data gives the melting point of a alloy of lead and zinc where ‘t’ is the temperature in degree c and P is the percentage of lead in the alloy.
| P | 40 | 50 | 60 | 70 | 80 | 90 |
| T | 180 | 204 | 226 | 250 | 276 | 304 |
Find the melting point of the alloy containing 84 percent lead.
Find f(2.8) from the following table:
| x | 0 | 1 | 2 | 3 |
| f(x) | 1 | 2 | 11 | 34 |
Choose the correct alternative:
Lagrange’s interpolation formula can be used for
Choose the correct alternative:
For the given data find the value of Δ3y0 is
| x | 5 | 6 | 9 | 11 |
| y | 12 | 13 | 15 | 18 |
A second degree polynomial passes though the point (1, –1) (2, –1) (3, 1) (4, 5). Find the polynomial
The area A of circle of diameter ‘d’ is given for the following values
| D | 80 | 85 | 90 | 95 | 100 |
| A | 5026 | 5674 | 6362 | 7088 | 7854 |
Find the approximate values for the areas of circles of diameter 82 and 91 respectively
If u0 = 560, u1 = 556, u2 = 520, u4 = 385, show that u3 = 465
Using Lagrange’s interpolation formula find a polynominal which passes through the points (0, –12), (1, 0), (3, 6) and (4, 12)
