Advertisements
Advertisements
Question
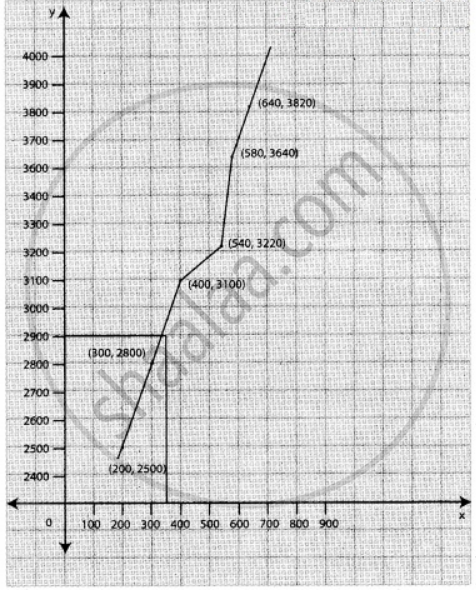
The following data relates to indirect labour expenses and the level of output
| Months | Jan | Feb | Mar |
| Units of output | 200 | 300 | 400 |
| Indirect labour expenses (Rs) |
2500 | 2800 | 3100 |
| Months | Apr | May | June |
| Units of output | 640 | 540 | 580 |
| Indirect labour expenses (Rs) |
3820 | 3220 | 3640 |
Estimate the expenses at a level of output of 350 units, by using graphic method.
Solution
APPEARS IN
RELATED QUESTIONS
In an examination the number of candidates who secured marks between certain intervals was as follows:
| Marks | 0 - 19 | 20 - 39 | 40 - 59 | 60 - 79 | 80 - 99 |
| No. of candidates |
41 | 62 | 65 | 50 | 17 |
Estimate the number of candidates whose marks are less than 70.
Find the value of f(x) when x = 32 from the following table:
| x | 30 | 5 | 40 | 45 | 50 |
| f(x) | 15.9 | 14.9 | 14.1 | 13.3 | 12.5 |
Using interpolation estimate the output of a factory in 1986 from the following data.
| Year | 1974 | 1978 | 1982 | 1990 |
| Output in 1000 tones |
25 | 60 | 80 | 170 |
Choose the correct alternative:
For the given points (x0, y0) and (x1, y1) the Lagrange’s formula is
Choose the correct alternative:
Lagrange’s interpolation formula can be used for
Choose the correct alternative:
For the given data find the value of Δ3y0 is
| x | 5 | 6 | 9 | 11 |
| y | 12 | 13 | 15 | 18 |
A second degree polynomial passes though the point (1, –1) (2, –1) (3, 1) (4, 5). Find the polynomial
Find the missing figures in the following table:
| x | 0 | 5 | 10 | 15 | 20 | 25 |
| y | 7 | 11 | - | 18 | - | 32 |
Find f(0.5) if f(– 1) = 202, f(0) = 175, f(1) = 82 and f(2) = 55
If u0 = 560, u1 = 556, u2 = 520, u4 = 385, show that u3 = 465
