Advertisements
Advertisements
प्रश्न
The maximum velocity of a particle performing linear S.H.M. is 0.16 m/s. If its maximum acceleration is 0.64 m/s2, calculate its period.
उत्तर
vmax = 0.16 m/s, amax =0.64 m/s2
Period (T) = ?
vmax = Aω and amax = Aω2
`a_max/v_max=omega=(2pi)/T`
`T=(2pixxv_max)/a_max`
`=(2xx3.14xx0.16)/0.64`
`= 1.571 s`
Period of particle is 1.571 s
APPEARS IN
संबंधित प्रश्न
A particle performing linear S.H.M. has a period of 6.28 seconds and a pathlength of 20 cm. What is the velocity when its displacement is 6 cm from mean position?
Define linear S.H.M.
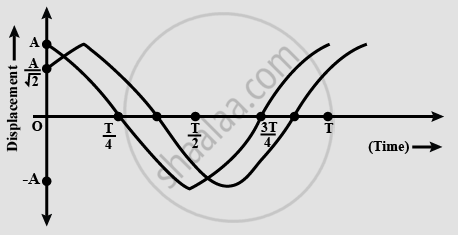
Two particles perform linear simple harmonic motion along the same path of length 2A and period T as shown in the graph below. The phase difference between them is ___________.
Obtain the differential equation of linear simple harmonic motion.
A particle executing linear S.H.M. has velocities v1 and v2 at distances x1 and x2 respectively from the mean position. The angular velocity of the particle is _______
A particle performing linear S.H.M. has the maximum velocity of 25 cm/s and maximum acceleration of 100 cm/ m2. Find the amplitude and period of oscillation. (π = 3.142)
From differential equation of linear S.H.M., obtain an expression for acceleration, velocity and displacement of a particle performing S.H.M.
In SI units, the differential equation of an S.H.M. is `("d"^2"x")/("dt"^2)` = − 36x. Find its frequency and period.
A body of mass m performs linear S.H.M. given by equation, x = P sin cot + Q sin`(omega"t" + pi/2)`. The total energy of the particle at any instant is ______.
A particle performing Linear S.H.M. has a maximum velocity 25 cm/sand maximum acceleration 100 cm/s2. Find the period of oscillations.
What is the rotational analogue of Newton's second law of motion?
The speeds of a particle performing linear SHM are 8 units and 6 units at respective displacements of 6 cm and 8 cm. Find its period and amplitude.
A spring balance has a scale that reads from 0 to 50 kg. The length of the scale is 20 cm. A body suspended from this balance, when displaced and released osillates with a period of 0.6 sec. What is the weight of the body?
