Advertisements
Advertisements
प्रश्न
The moment of inertia of a body about a given axis is 1.2 kgm2. initially, the body is at rest. For what duration on the angular acceleration of 25 radian/sec2 must be applied about that axis in order to produce rotational kinetic energy of 1500 joule?
उत्तर
Given:
I = 1.2 kgm2, α = 25 radian/sec2, ω0 = 0 rad/s, (K.E.)rot = 1500 J
To find: Time (t)
Formulae:
i. α = `(ω - ω_0)/t`
ii. K.E. = `1/2"Iω"^2`
Calculation:
From formula (i),
25 = `(ω - 0)/t`
∴ ω = 25t
From formula (ii),
1500 = `1/2 xx 1.2 xx (25t)^2`
∴ t = `sqrt((2 xx 1500)/(1.2 xx 25^2)) = sqrt4`
∴ t = 2 sec.
An angular acceleration must be applied for 2 sec.
APPEARS IN
संबंधित प्रश्न
A diver in a swimming pool bends his head before diving. It ______
The moment of inertia of a circular loop of radius R, at a distance of R/2 around a rotating axis parallel to horizontal diameter of the loop is ______
Two wheels of the moment of inertia 4 kgm2 rotate side by side at the rate of 120 rev/min and 240 rev/min respectively in the opposite directions. If now both the wheels are coupled by means of a weightless shaft so that both the wheels rotate with a common angular speed. Calculate the new speed of rotation.
A uniform disc of radius ' a' and mass 'm' is rotating freely with angular speed 'ω' in a horizontal plane, about a smooth fixed vertical axis through its centre. A pa1ticle of mass 'm' is then suddenly attached to the rim of the disc and rotates with it. The new angular speed is ______
Surface density of charge on a charged conducting sphere of radius R in terms of electric field intensity E at a distance r in free space is ____________.
(r > R, ε0 = permittivity of free space)
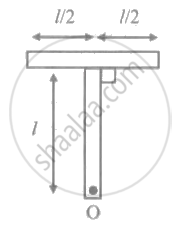
Two rods, each of mass m and length l, are joined as shown in the figure. Moment of inertia of system about an axis passing through one end of the rod, i.e. O, and perpendicular to the plane is ____________.
Four solid spheres each of mass M and radius R are placed with their centres on the four comers of a rectangle. If b is a breadth of rectangle and its length is twice of its breadth, then find moment of inertia of the system about an axis along one of the breadth of the rectangle.
Three identical rods each of mass 'M' and length 'L' are joined to form a symbol 'H'. The moment of inertia of the system about one of the sides of 'H' is ______.
A particle is performing U.C.M. along the circumference of a circle of diameter 50 cm with frequency 2 Hz. The acceleration of the particle in m/s2 is ______.
If I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia of the ring formed by bending the rod about an axis perpendicular to the plane, the ratio of I1 and I2 is ____________.
Moment of inertia of earth about its axis of rotation is ____________.
From a disc of mass 'M' and radius 'R', a circular hole of diameter 'R' is cut whose rim passes through the center. The moment of inertia of the remaining part of the ruse about perpendicular axis passing through the center is ______.
A cord is wound round the circumference of a wheel of radius 'r'. The axis of the wheel is horizontal and moment of inertia about it is T. A block of mass 'm' is attached to free end of the cord, initially at rest. When the wheel rotates and the block moves vertically downwards through distance 'h', the angular velocity of the wheel will be ______.
(Neglect the mass of cord, g =acceleration due to gravity)
The moment of inertia of a body initially at rest about a given axis is 1.2 kg m2. On applying an acceleration of 25 rad/s2, the time it will take to acquire a rotational kinetic energy of 1500 J is ____________.
A rod of length 1 m and mass `1/2` kg rotates at an 2 angular speed of 6 rad s-1 about one of its ends. The kinetic energy of the rod is ______.
The moment of inertia of a sphere is 20 kg-m2 about the diameter. The moment of inertia about any tangent is ____________.
A disc of mass 100 kg and radius 1 m is rotating at 300 rpm. The torque required to rotate the disc in opposite direction with same speed in time 50 second is ______.
Two discs having moment of inertia I1 and I2 are made from same material have same mass. Their thickness and radii are t1, t2, and R1, R2 respectively. The relation between moment of inertia of each disc about an axis passing through its centre and perpendicular to its plane and its thickness is ______.
A thin uniform rod of length 'L' and mass 'M' is bent at the middle point 'O' at an angle of 45° as shown in the figure. The moment of inertia of the system about an axis passing through 'O' and perpendicular to the plane of the bent rod, is ______.
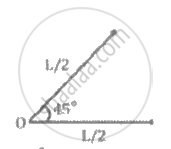
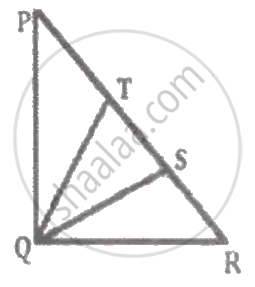
Figure shows triangular lamina which can rotate about different axis of rotation. Moment of inertia is maximum about the axis ______.
A disc rolls down a smooth inclined plane without slipping. An inclined plane makes an angle of 60° with the vertical. The linear acceleration of the disc along the inclined plane is ______.
(g = acceleration due to gravity, sin 30° =cos 60° `=1/2,` sin 60° = cos 30° `=sqrt3/2`)
For the same cross-sectional area and for a given load, the ratio of depressions for the beam of a square cross-section and circular cross-section is ______.
The moment of inertia of a body about a given axis is 1.2 kg-m2. Initially, the body is at rest. In order to produce, a rotational kinetic energy of 1500 J, an acceleration of 25 rad/s2 must be applied about that axis for a duration of ______.
The moment of inertia (MI) of a disc of radius R and mass M about its central axis is ______.
