Advertisements
Advertisements
Question
The moment of inertia of a body about a given axis is 1.2 kgm2. initially, the body is at rest. For what duration on the angular acceleration of 25 radian/sec2 must be applied about that axis in order to produce rotational kinetic energy of 1500 joule?
Solution
Given:
I = 1.2 kgm2, α = 25 radian/sec2, ω0 = 0 rad/s, (K.E.)rot = 1500 J
To find: Time (t)
Formulae:
i. α = `(ω - ω_0)/t`
ii. K.E. = `1/2"Iω"^2`
Calculation:
From formula (i),
25 = `(ω - 0)/t`
∴ ω = 25t
From formula (ii),
1500 = `1/2 xx 1.2 xx (25t)^2`
∴ t = `sqrt((2 xx 1500)/(1.2 xx 25^2)) = sqrt4`
∴ t = 2 sec.
An angular acceleration must be applied for 2 sec.
APPEARS IN
RELATED QUESTIONS
A diver in a swimming pool bends his head before diving. It ______
Two bodies have their moments of inertia I and 2I respectively about their axis of rotation. If their kinetic energies of rotation are equal, then what is the ratio of their angular velocity.
The moment of inertia of a uniform circular disc about a tangent in its own plane is 5/4MR2 where M is the mass and R is the radius of the disc. Find its moment of inertia about an axis through its centre and perpendicular to its plane.
Two wheels of the moment of inertia 4 kgm2 rotate side by side at the rate of 120 rev/min and 240 rev/min respectively in the opposite directions. If now both the wheels are coupled by means of a weightless shaft so that both the wheels rotate with a common angular speed. Calculate the new speed of rotation.
A particle starting from rest moves along the circumference of a circle of radius r with angular acceleration a. The magnitude of the average velocity, in the time it completes the small angular displacement θ is
The moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L/3 from one of its ends and perpendicular to the rod is ______
Three points masses, each of mass m are placed at the corners of an equilateral triangle of side l. The moment of inertia of the system about an axis passing through one of the vertices and parallel to the side joining other two vertices, will be ______.
If radius of the solid sphere is doubled by keeping its mass constant, the ratio of their moment of inertia about any of its diameter is ______.
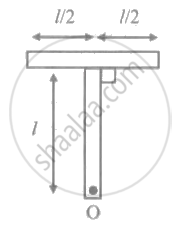
Two rods, each of mass m and length l, are joined as shown in the figure. Moment of inertia of system about an axis passing through one end of the rod, i.e. O, and perpendicular to the plane is ____________.
Four solid spheres each of mass M and radius R are placed with their centres on the four comers of a rectangle. If b is a breadth of rectangle and its length is twice of its breadth, then find moment of inertia of the system about an axis along one of the breadth of the rectangle.
Three identical rods each of mass 'M' and length 'L' are joined to form a symbol 'H'. The moment of inertia of the system about one of the sides of 'H' is ______.
A flywheel of mass 20 kg and radius 5 cm is revolving at a speed of 300 rpm. Its kinetic energy is ______.
If I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia of the ring formed by bending the rod about an axis perpendicular to the plane, the ratio of I1 and I2 is ____________.
Moment of inertia of earth about its axis of rotation is ____________.
A cord is wound round the circumference of a wheel of radius 'r'. The axis of the wheel is horizontal and moment of inertia about it is T. A block of mass 'm' is attached to free end of the cord, initially at rest. When the wheel rotates and the block moves vertically downwards through distance 'h', the angular velocity of the wheel will be ______.
(Neglect the mass of cord, g =acceleration due to gravity)
The moment of inertia of a body initially at rest about a given axis is 1.2 kg m2. On applying an acceleration of 25 rad/s2, the time it will take to acquire a rotational kinetic energy of 1500 J is ____________.
A rod of length 1 m and mass `1/2` kg rotates at an 2 angular speed of 6 rad s-1 about one of its ends. The kinetic energy of the rod is ______.
Three rings, each of mass P and radius Q, are arranged as shown in the figure. The moment of inertia of the arrangement about YY' will be ______.

The moment of inertia of a sphere is 20 kg-m2 about the diameter. The moment of inertia about any tangent is ____________.
Two discs having moment of inertia I1 and I2 are made from same material have same mass. Their thickness and radii are t1, t2, and R1, R2 respectively. The relation between moment of inertia of each disc about an axis passing through its centre and perpendicular to its plane and its thickness is ______.
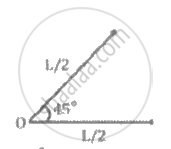
A thin uniform rod of length 'L' and mass 'M' is bent at the middle point 'O' at an angle of 45° as shown in the figure. The moment of inertia of the system about an axis passing through 'O' and perpendicular to the plane of the bent rod, is ______.
The moment of inertia of a ring about an axis passing through its centre and perpendicular to its plane is 'I'. It is rotating with angular velocity 'ω'. Another identical ring is gently placed on it so that their centres coincide. If both the ring are rotating about the same axis, then loss in kinetic energy is ______.
A uniform disc of mass 4 kg has radius of 0.4 m. Its moment of inertia about an axis passing through a point on its circumference and perpendicular to its plane is ______.
A disc rolls down a smooth inclined plane without slipping. An inclined plane makes an angle of 60° with the vertical. The linear acceleration of the disc along the inclined plane is ______.
(g = acceleration due to gravity, sin 30° =cos 60° `=1/2,` sin 60° = cos 30° `=sqrt3/2`)
A thin circular ring of mas 'M' and radius 'R' is rotating about a transverse axis passing through its centre with constant angular velocity 'ω'. Two objects each of mass 'm' are attached gently to the opposite ends of a diameter of the ring. What is the new angular velocity?
The moment of inertia of a circular disc of mass M and radius R about an axis passing through the centre of mass is I0. The moment of inertia of another circular disc of same mass and thickness but half the density about the same axis is ______.
For the same cross-sectional area and for a given load, the ratio of depressions for the beam of a square cross-section and circular cross-section is ______.
