Question

The zeroes of the quadratic polynomial x² + kx + k, k ≠ 0 ______.

पर्याय

• Cannot both be positive

• Cannot both be negative

• Are always unequal

• Are always equal

Answer 1

The zeroes of the quadratic polynomial x² + kx + k, k ≠ 0 cannot both be positive.

Explanation:

Let p(x) = x² + kx + k, k ≠ 0

On comparing p(x) with ax² + bx + c, we get

Now, a = 1, b = k and c = k

`x = (-b +- sqrt(b^2 - 4ac))/(2a)`   ....[By quadratic formula]

= `(-k +- sqrt(k^2 - 4k))/(2 xx 1)`

= `(-k +- sqrt(k(k - 4)))/2, k ≠ 0`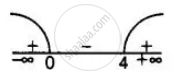

Here, we see that

k(k − 4) > 0

⇒ `k ∈ (-oo, 0)  u  (4, oo)`

Now, we know that

In quadratic polynomial ax² + bx + c

If a > 0

b > 0

c > 0

or a < 0

b < 0

c < 0

Then the polynomial has always all negative zeroes.

And if a > 0, c < 0 or a < 0, c > 0

Then the polynomial has always zeroes of opposite sign

Case I: If `k ∈ (-oo, 0)`

i.e., k < 0

⇒ a = 1 > 0, b, c = k < 0

So, both zeroes are of opposite sign.

Case II: If `k ∈ (4, oo)`

i.e., k ≥ 4

⇒ a = 1 > 0, b, c > 4

So, both zeroes are negative.

Hence, in any case zeroes of the given quadratic polynomial cannot both be positive.