Advertisements
Advertisements
प्रश्न
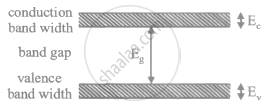
There are energy bands in a solid. Do we have really continuous energy variation in a band ro do we have very closely spaced but still discrete energy levels?
उत्तर
A solid consists of a combination of closely spaced energy levels. These energy levels are discrete but they have very small energy gap between two consecutive levels so they are reffered as band.However, the energy levels in the band are discrete.
APPEARS IN
संबंधित प्रश्न
Distinguish between a conductor and a semi conductor on the basis of energy band diagram
In semiconductors, thermal collisions are responsible for taking a valence electron to the conduction band. Why does the number of conduction electrons not go on increasing with time as thermal collisions continuously take place?
When an electron goes from the valence band to the conduction band in silicon, its energy is increased by 1.1 eV. The average energy exchanged in a thermal collision is of the order of kT which is only 0.026 eV at room temperature. How is a thermal collision able to take some to the electrons from the valence band to the conduction band?
We have valence electrons and conduction electrons in a semiconductor. Do we also have 'valence holes' and 'conduction holes'?
Let np and ne be the number of holes and conduction electrons in an intrinsic semiconductor.
When an impurity is doped into an intrinsic semiconductor, the conductivity of the semiconductor
In a transistor,
In a semiconductor,
(a) there are no free electrons at 0 K
(b) there are no free electrons at any temperature
(c) the number of free electrons increases with temperature
(d) the number of free electrons is less than that in a conductor.
The impurity atoms with which pure silicon may be doped to make it a p-type semiconductor are those of
(a) phosphorus
(b) boron
(c) antimony
(d) aluminium.
A semiconductor is doped with a donor impurity.
Indium antimonide has a band gap of 0.23 eV between the valence and the conduction band. Find the temperature at which kT equals the band gap.
When a semiconducting material is doped with an impurity, new acceptor levels are created. In a particular thermal collision, a valence electron receives an energy equal to 2kT and just reaches one of the acceptor levels. Assuming that the energy of the electron was at the top edge of the valence band and that the temperature T is equal to 300 K, find the energy of the acceptor levels above the valence band.
The conductivity of an intrinsic semiconductor depends on temperature as σ = σ0e−ΔE/2kT, where σ0 is a constant. Find the temperature at which the conductivity of an intrinsic germanium semiconductor will be double of its value at T = 300 K. Assume that the gap for germanium is 0.650 eV and remains constant as the temperature is increased.
(Use Planck constant h = 4.14 × 10-15 eV-s, Boltzmann constant k = 8·62 × 10-5 eV/K.)
A semiconducting material has a band gap of 1 eV. Acceptor impurities are doped into it which create acceptor levels 1 meV above the valence band. Assume that the transition from one energy level to the other is almost forbidden if kT is less than 1/50 of the energy gap. Also if kT is more than twice the gap, the upper levels have maximum population. The temperature of the semiconductor is increased from 0 K. The concentration of the holes increases with temperature and after a certain temperature it becomes approximately constant. As the temperature is further increased, the hole concentration again starts increasing at a certain temperature. Find the order of the temperature range in which the hole concentration remains approximately constant.
(Use Planck constant h = 4.14 × 10-15 eV-s, Boltzmann constant k = 8·62 × 10-5 eV/K.)
Hydrogen atom in n = 3 state has a lifetime of 10-10 sec. The number of revolutions an electron makes in the n = 3 state before returning to the ground state is ______.
Useful data
`1/(4pi∈_0) = 8.99 xx 10^-34`N m2 C-2; e = 1.60 10-19 C; h = 6.63 10-34 Js; me = 9 × 10-3 kg
If the lattice constant of this semiconductor is decreased, then which of the following is correct?
The energy of a hydrogen atom in the ground state is −13.6 eV. The energy of a He+ ion in the first excited state will be:
A semiconductor is cooled from T.K to T2K its resistance will
In a common base configuration Ie = 1 mA α = 0.95 the value of base current is
