Advertisements
Advertisements
प्रश्न
To study the decomposition of hydrogen iodide, a student fills an evacuated 3 litre flask with 0.3 mol of HI gas and allows the reaction to proceed at 500°C. At equilibrium he found the concentration of HI which is equal to 0.05 M. Calculate Kc and Kp.
उत्तर
V = 3 L
`["HI"]_"initial" = (0.3 "mol")/(3"L")` 0.1 M
[HI]eq = 0.05 M
\[\ce{2 HI(g) <=> H2(g) + l_2(g)}\]
| HI (g) | H2 (g) | I2 (g) | |
| Initial concentration | 0.1 | - | - |
| Reacted | 0.05 | - | - |
| Equilibrium concentration | 0.05 | 0.025 | 0.025 |
`"K"_"C" =(["H"_2]["I"_2])/(["HI"]^2)`
`= (0.025 xx 0.025)/(0.05 xx 0.05)` = 0.25
Kp = Kc(RT)(∆ng)
∆ng = 2 – 2 = 0
Kp = 0.25(RT)0
Kp = 0.25.
APPEARS IN
संबंधित प्रश्न
`"K"_"C"/"K"_"P"` for the reaction,
\[\ce{N2(g) + 3H2(g) <=> 2NH3(g)}\] is
In which of the following equilibrium, Kp and Kc are not equal?
The values of Kp1 and Kp2; for the reactions,
X ⇌ Y + Z,
A ⇌ 2B are in the ratio 9 : 1 if degree of dissociation of X and A be equal then total pressure at equilibrium P1, and P2 are in the ratio
\[\ce{[CO(H2O)6]^2+ (aq) (pink) + 4Cl- (aq) <=> [CoCl4]^2- (aq) (blue) + 6 H2O (l)}\]
In the above reaction at equilibrium, the reaction mixture is blue in colour at room temperature. On cooling this mixture, it becomes pink in color. On the basis of this information, which one of the following is true?
What is the relation between Kp and Kc? Given one example for which Kp is equal to Kc.
For the reaction, \[\ce{A2(g) + B2(g) <=> 2AB(g); \Delta H}\] is -ve.
the following molecular scenes represent differenr reaction mixture. (A-green, B-blue)
| Closed ← |
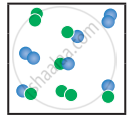 |
 |
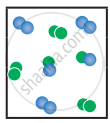 |
| System | At equilibrium | (x) | (y) |
- Calculate the equilibrium constant Kp and (Kc).
- For the reaction mixture represented by scene (x), (y) the reaction proceed in which directions?
- What is the effect of an increase in pressure for the mixture at equilibrium?
One mole of PCl5 is heated in one litre closed container. If 0.6 mole of chlorine is found at equilibrium, Calculate the value of equilibrium constant.
At particular temperature Kc = 4 × 10-2 for the reaction, \[\ce{H2S (g) <=> H2(g) +1/2 S2(g)}\]. Calculate the Kc for the following reaction.
\[\ce{2H2S (g) <=> 2H2 (g) + S2 (g)}\]
The equilibrium for the dissociation of XY2 is given as,
\[\ce{2 XY2 (g) <=> 2 XY (g) + Y2 (g)}\]
if the degree of dissociation x is so small compared to one. Show that 2 Kp = PX3 where P is the total pressure and Kp is the dissociation equilibrium constant of XY2.
The partial pressure of carbon dioxide in the reaction
\[\ce{CaCO3(s) <=> CaO(s) + CO2(g)}\] is 1.017 × 10-3 atm at 500°C. Calculate Kp at 600°C for the reaction. H for the reaction is 181 KJ mol-1 and does not change in the given range of temperature.
