Advertisements
Advertisements
प्रश्न
त्रिकोणाच्या तीन कोनांची मापे अंकगणिती श्रेढरीमध्ये आहेत. सर्वांत लहान कोनाचे माप साधारण फरकाच्या पाचपट आहे, तर त्या त्रिकोणाच्या तीनही कोनांची मापे काढा. (त्रिकोणाच्या कोनांची मापे a, a + d, a + 2d घ्या.)
उत्तर
समजा, त्रिकोणाच्या तीन कोनांची मापे अंकगणिती श्रेढीत अनुक्रमे a, a + d, a + 2d, आहेत.
येथे a = पहिले पद, d = साधारण फरक
त्रिकोणाच्या कोनांच्या मापांची बेरीज 180° असते.
∴ a + a + d + a + 2d = 180°
∴ 3a + 3d = 180°
∴ a + d = `180^circ/3`
∴ a + d = 60° ...(i)
दिलेल्या अटीनुसार, सर्वांत लहान कोनाचे माप साधारण फरकाच्या पाचपट आहे.
∴ a = 5d
a = 5d समीकरण (i) मध्ये ठेवून,
5d + d = 60°
∴ 6d = 60°
∴ d = `60^circ/6` = 10°
∴ a = 5d = 5(10°) = 50°
a + d = 50° + 10° = 60°
a + 2d = 50° + 2(10°)
= 50° + 20°
= 70°
∴ त्रिकोणाच्या तीनही कोनांची मापे 50°, 60° व 70° आहेत.
APPEARS IN
संबंधित प्रश्न
1 व 140 यांच्या दरम्यान, 4 ने भाग जाणाऱ्या नैसर्गिक संख्यांची बेरीज किती आहे, हे काढण्यासाठी खालील कृती पूर्ण करा.
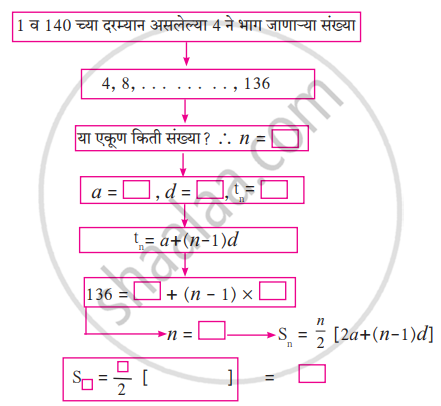
1 व 140 यांच्या दरम्यान 4 ने भाग जाणाऱ्या संख्यांची बेरीज = `square`
एका अंकगणिती श्रेढीच्या पहिल्या 55 पदांची बेरीज 3300 आहे, तर तिचे 28 वे पद काढा.
एका अंकगणिती श्रेढीतील तीन क्रमागत पदांची बेरीज 27 व त्यांचा गुणाकार 504 आहे, तर ती पदे शोधा.
(तीन क्रमागत पदे a - d, a, a + d माना.)
एका अंकगणिती श्रेढीतील चार क्रमागत पदांची बेरीज 12 आहे. तसेच, त्या चार क्रमागत पदांपैकी तिसऱ्या व चौथ्या पदांची बेरीज 14 आहे, तर ती चार पदे काढा.
(चार क्रमागत पदे a - d, a, a + d, a + 2d माना.)
12, 14, 16, 18, 20, ......... या अंकगणिती श्रेढीच्या पहिल्या 100 पदांची बेरीज करा.
कृती: येथे, a = 12, d = `square` n = 100, S100 = ?
Sn = `"n"/2[square + ("n" - 1)"d"]`
S100 = `square/2`[24 + (100 – 1)d]
= 50 (24 + `square`)
= `square`
= `square`
1 ते 140 यांदरम्यानच्या 4 ने भाग जाणाऱ्या नैसर्गिक संख्यांची बेरीज करा.
कृती: 1 ते 140 यांदरम्यानच्या 4 ने भाग जाणाऱ्या नैसर्गिक संख्या 4, 8, 12, 16......... 136 या आहेत.
येथे, d = 4 आहे. म्हणून, दिलेली क्रमिका ही अंकगणिती श्रेढी आहे.
a = 4, d = 4, tn = 136, Sn = ?
tn = a + (n – 1) d
`square` = 4 + (n – 1) × 4
`square` = (n –1) × 4
n = `square`
आता, Sn = `"n"/2` + [a + tn]
Sn = 17 × `square`
Sn = `square`
म्हणून, 1 ते 140 यांदरम्यानच्या 4 ने भाग जाणाऱ्या नैसर्गिक संख्यांची बेरीज `square` आहे.
4 ने भाग जाणाऱ्या तीन अंकी नैसर्गिक संख्यांची बेरीज काढा.
1 ते 50 मधील सर्व विषम संख्यांची बेरीज करा.
1 + 3 + 5 + ......... + 101 या 1 ते 101 पर्यंत विषम नैसर्गिक संख्यांची बेरीज करा.
पहिल्या 'n' सम नैसर्गिक संख्यांची बेरीज करा.
