Advertisements
Advertisements
प्रश्न
Two concentric circular loops of radius 1 cm and 20 cm are placed coaxially.
(i) Find mutual inductance of the arrangement.
(ii) If the current passed through the outer loop is changed at a rate of 5 A/ms, find the emf induced in the inner loop. Assume the magnetic field on the inner loop to be uniform.
उत्तर
We know `varphi = "MI"`
And magnetic field at the center of the bigger loop `vec"B" = (mu_o"I")/(2"R") = (4pi xx 10^-7"I")/(2xx20xx10^-2) = pi xx 10^-6"I"`
Flux through the smaller loop
`varphi = "BA"_"s" = (4pixx10^-5"I")/40 xx pi(0.01)^2 = pi^2 xx 10^-10 xx "I"`
`"M" = varphi/"I" = pi^2 xx 10^-10 = 9.86 xx 10^-10 "H"`
Now emf induced
e = `-("d"varphi)/("d""t") = -9.86 xx 10^-10 xx ("d""I")/("d""t")`
e = `-9.86 xx 10^-10 xx 5 = -4.93 xx 10^-9 "V"`
APPEARS IN
संबंधित प्रश्न
State Biot-Savart law.
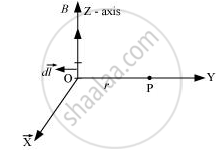
A current I flows in a conductor placed perpendicular to the plane of the paper. Indicate the direction of the magnetic field due to a small element d `vecl` at point P situated at distance `vecr` from the element as shown in the figure.
A wire of length l is bent in the form of an equilateral triangle and carries an electric current i. Find the magnetic field B at the centre.
A regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic filed B at the centre of the polygon. (b) By letting n → ∞, deduce the expression for the magnetic field at the centre of a circular current.
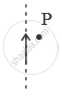
An electric current I flows through an infinitely long conductor as shown in Figure 2 (a) below. Write an expression and direction for the magnetic field at point P.
State and explain the law used to determine magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current carrying loop of radius r at its centre.
A long wire with a small current element of length 1 cm is placed at the origin and carries a current of 10 A along the X-axis. Find out the magnitude and direction of the magnetic field due to the element on the Y-axis at a distance 0.5 m from it.
A straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the figure. Find the magnitude and direction of the magnetic field at the centre of the arc.

State Biot Savart law.
Biot-Sawart law indicates that the moving electrons (velocity `overset(->)("v")`) produce a magnetic field B such that
A current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin, joined together. Find the direction and magnitude of B at the origin.
