Advertisements
Advertisements
प्रश्न
Two particles A and B, each carrying a charge Q, are held fixed with a separation dbetween them. A particle C of mass m and charge q is kept at the middle point of the line AB. If it is displaced through a distance x perpendicular to AB, what would be the electric force experienced by it?
उत्तर
The charge q is displaced by a distance x on the perpendicular bisector of AB.
As shown in the figure, the horizontal component of the force is balanced.
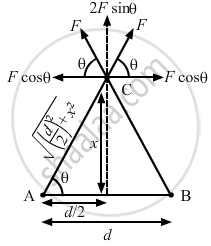
\[\sin\theta = \frac{x}{\sqrt{\left( \frac{d}{2} \right)^2 + x^2}}\]
Total vertical component of the force,
\[F' = 2F\sin\theta\]
\[F' = 2 \times \frac{1}{4\pi \epsilon_0} \times \frac{qQ}{\left( \frac{d}{2} \right)^2 + x^2} \times \frac{x}{\sqrt{\left( \frac{d}{2} \right)^2 + x^2}}\]
\[ \Rightarrow F' = \frac{1}{2\pi \epsilon_0} \times \frac{qQx}{\left[ \left( \frac{d}{2} \right)^2 + x^2 \right]^{3/2}}\]
This is the net electric force experienced by the charge q.
APPEARS IN
संबंधित प्रश्न
Check that the ratio ke2/G memp is dimensionless. Look up a Table of Physical Constants and determine the value of this ratio. What does the ratio signify?
Four point charges qA = 2 μC, qB = −5 μC, qC = 2 μC, and qD = −5 μC are located at the corners of a square ABCD of side 10 cm. What is the force on a charge of 1 μC placed at the centre of the square?
Three-point charges q, – 4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q

(b) Find out the amount of the work done to separate the charges at infinite distance.
At what separation should two equal charges, 1.0 C each, be placed, so that the force between them equals the weight of a 50 kg person?
One end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and a charge of 4.0× 10-6 C. In equilibrium, the thread makes an angle of 60° with the vertical. Find the surface charge density on the plate.
Two charged particles are placed 1.0 cm apart. What is the minimum possible magnitude of the electric force acting on each charge?
Estimate the number of electrons in 100 g of water. How much is the total negative charge on these electrons?
Two insulating small spheres are rubbed against each other and placed 1 cm apart. If they attract each other with a force of 0.1 N, how many electrons were transferred from one sphere to the other during rubbing?
Two identical pith balls are charged by rubbing one against the other. They are suspended from a horizontal rod through two strings of length 20 cm each, the separation between the suspension points being 5 cm. In equilibrium, the separation between the balls is 3 cm. Find the mass of each ball and the tension in the strings. The charge on each ball has a magnitude 2.0 × 10−8 C.
A particle A with a charge of 2.0 × 10−6 C is held fixed on a horizontal table. A second charged particle of mass 80 g stays in equilibrium on the table at a distance of 10 cm from the first charge. The coefficient of friction between the table and this second particle is μ = 0.2. Find the range within which the charge of this second particle may lie.
Two charged particles, with equal charges of 2.0 × 10−5 C, are brought from infinity to within a separation of 10 cm. Find the increase in the electric potential energy during the process
How much work has to be done in assembling three charged particles at the vertices of an equilateral triangle, as shown in the figure?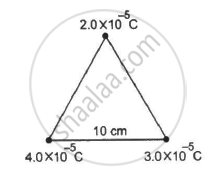
Define a unit charge.
Write down Coulomb’s law in vector form and mention what each term represents.
Two point charges +3 µC and +8 µC repel each other with a force of 40 N. If a charge of -5 µC is added to each of them, then force between them will become ______.
The unit of charge is ______.
Two identical thin rings, each of radius a meter, are coaxially placed at a distance R meter apart. If Q1 coulomb and Q2 coulomb are respectively the charges uniformly spread on the two rings, the work done in moving a charge q coulomb from the centre of one ring to that of the other is ______.
Coulomb's law is given by F = k q1q2 rn where n is
There is another useful system of units, besides the SI/mks A system, called the cgs (centimeter-gram-second) system. In this system Coloumb’s law is given by
F = `(Qq)/r^2 hatr`
where the distance r is measured in cm (= 10–2 m), F in dynes (= 10–5 N) and the charges in electrostatic units (es units), where 1 es unit of charge = `1/([3]) xx 10^-9 C`
The number [3] actually arises from the speed of light in vaccum which is now taken to be exactly given by c = 2.99792458 × 108 m/s. An approximate value of c then is c = [3] × 108 m/s.
(i) Show that the coloumb law in cgs units yields
1 esu of charge = 1 (dyne)1/2 cm.
Obtain the dimensions of units of charge in terms of mass M, length L and time T. Show that it is given in terms of fractional powers of M and L.
(ii) Write 1 esu of charge = x C, where x is a dimensionless number. Show that this gives
`1/(4pi ∈_0) = 10^-9/x^2 (N*m^2)/C^2`
With `x = 1/([3]) xx 10^-9`, we have `1/(4pi ∈_0) = [3]^2 xx 10^9 (Nm^2)/C^2`
or, `1/(4pi ∈_0) = (2.99792458)^2 xx 10^9 (Nm^2)/C^2` (exactly).
