Advertisements
Advertisements
प्रश्न
Two particles A and B, each carrying a charge Q, are held fixed with a separation dbetween them. A particle C of mass m and charge q is kept at the middle point of the line AB. If it is displaced through a distance x perpendicular to AB, what would be the electric force experienced by it?
उत्तर
The charge q is displaced by a distance x on the perpendicular bisector of AB.
As shown in the figure, the horizontal component of the force is balanced.
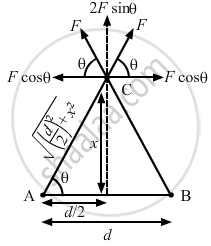
\[\sin\theta = \frac{x}{\sqrt{\left( \frac{d}{2} \right)^2 + x^2}}\]
Total vertical component of the force,
\[F' = 2F\sin\theta\]
\[F' = 2 \times \frac{1}{4\pi \epsilon_0} \times \frac{qQ}{\left( \frac{d}{2} \right)^2 + x^2} \times \frac{x}{\sqrt{\left( \frac{d}{2} \right)^2 + x^2}}\]
\[ \Rightarrow F' = \frac{1}{2\pi \epsilon_0} \times \frac{qQx}{\left[ \left( \frac{d}{2} \right)^2 + x^2 \right]^{3/2}}\]
This is the net electric force experienced by the charge q.
APPEARS IN
संबंधित प्रश्न
Does the force on a charge due to another charge depend on the charges present nearby?
Consider a gold nucleus to be a sphere of radius 6.9 fermi in which protons and neutrons are distributed. Find the force of repulsion between two protons situated at largest separation. Why do these protons not fly apart under this repulsion?
Find the speed of the electron in the ground state of a hydrogen atom. The description of ground state is given in the previous problem.
Ten positively-charged particles are kept fixed on the x-axis at points x = 10 cm, 20 cm, 30 cm, ...., 100 cm. the first particle has a charge 1.0 × 10−8 C, the second 8 × 10−8 C, the third 27 × 10−8 C and so on. The tenth particle has a charge 1000 × 10−8 C. Find the magnitude of the electric force acting on a 1 C charge placed at the origin.
Two identical balls, each with a charge of 2.00 × 10−7 C and a mass of 100 g, are suspended from a common point by two insulating strings, each 50 cm long. The balls are held at a separation 5.0 cm apart and then released. Find.
(a) the electric force on one of the charged balls
(b) the components of the resultant force on it along and perpendicular to the string
(c) the tension in the string
(d) the acceleration of one of the balls. Answers are to be obtained only for the instant just after the release.
A particle A with a charge of 2.0 × 10−6 C and a mass of 100 g is placed at the bottom of a smooth inclined plane of inclination 30°. Where should another particle B, with the same charge and mass, be placed on the incline so that it may remain in equilibrium?
Two particles A and B possessing charges of +2.00 × 10−6 C and of −4.00 × 10−6 C, respectively, are held fixed at a separation of 20.0 cm. Locate the points (s) on the line AB, where (a) the electric field is zero (b) the electric potential is zero.
A point charge produces an electric field of magnitude 5.0 NC−1 at a distance of 40 cm from it. What is the magnitude of the charge?
How much work has to be done in assembling three charged particles at the vertices of an equilateral triangle, as shown in the figure?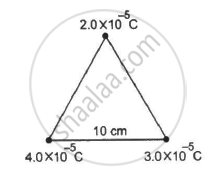
Two particles of masses 5.0 g each and opposite charges of +4.0 × 10−5 C and −4.0 × 10−5 C are released from rest with a separation of 1.0 m between them. Find the speeds of the particles when the separation is reduced to 50 cm.
Define a unit charge.
Write a short note on superposition principle.
Three charges +Q, q, +Q are placed respectively, at distance, 0, d/2 and d from the origin, on the X-axis. If the net force experienced by +Q, placed at x = 0, is zero then value of q is ____________.
A total charge Q is broken in two parts Q1 and Q2 and they are placed at a distance R from each other. The maximum force of repulsion between them will occur, when ____________.
Two point charges +3 µC and +8 µC repel each other with a force of 40 N. If a charge of -5 µC is added to each of them, then force between them will become ______.
The unit of charge is ______.
Coulomb's law is given by F = k q1q2 rn where n is
Two charge – 10c and + 10 c are placed 10 cm apart. Potential at centre of the line joining the two charge is:-
There is another useful system of units, besides the SI/mks A system, called the cgs (centimeter-gram-second) system. In this system Coloumb’s law is given by
F = `(Qq)/r^2 hatr`
where the distance r is measured in cm (= 10–2 m), F in dynes (= 10–5 N) and the charges in electrostatic units (es units), where 1 es unit of charge = `1/([3]) xx 10^-9 C`
The number [3] actually arises from the speed of light in vaccum which is now taken to be exactly given by c = 2.99792458 × 108 m/s. An approximate value of c then is c = [3] × 108 m/s.
(i) Show that the coloumb law in cgs units yields
1 esu of charge = 1 (dyne)1/2 cm.
Obtain the dimensions of units of charge in terms of mass M, length L and time T. Show that it is given in terms of fractional powers of M and L.
(ii) Write 1 esu of charge = x C, where x is a dimensionless number. Show that this gives
`1/(4pi ∈_0) = 10^-9/x^2 (N*m^2)/C^2`
With `x = 1/([3]) xx 10^-9`, we have `1/(4pi ∈_0) = [3]^2 xx 10^9 (Nm^2)/C^2`
or, `1/(4pi ∈_0) = (2.99792458)^2 xx 10^9 (Nm^2)/C^2` (exactly).
