Advertisements
Advertisements
प्रश्न
A point charge produces an electric field of magnitude 5.0 NC−1 at a distance of 40 cm from it. What is the magnitude of the charge?
उत्तर
Given:
Magnitude of the electric field, E = 5.0 NC−1 at a distance, r = 40 cm = 0.4 m
Let the magnitude of the charge be q .
\[E = \frac{1}{4\pi \epsilon_0}\frac{q}{r^2}\]
\[ \Rightarrow 5 . 0 = 9 \times {10}^9 \times \frac{q}{\left( 0 . 4 \right)^2}\]
\[ \Rightarrow q = 8 . 9 \times {10}^{- 11} C\]
APPEARS IN
संबंधित प्रश्न
Plot a graph showing the variation of coulomb force (F) versus ,`(1/r^2)` where r is the distance between the two charges of each pair of charges: (1 μC, 2 μC) and (2 μC, − 3 μC). Interpret the graphs obtained.
Find the dimensional formula of ε0.
Consider a gold nucleus to be a sphere of radius 6.9 fermi in which protons and neutrons are distributed. Find the force of repulsion between two protons situated at largest separation. Why do these protons not fly apart under this repulsion?
Suppose an attractive nuclear force acts between two protons which may be written as F=Ce−kr/r2. Write down the dimensional formulae and appropriate SI units of C and k.
Three equal charges, 2.0 × 10−6 C each, are held at the three corners of an equilateral triangle of side 5 cm. Find the Coulomb force experienced by one of the charges due to the other two.
Two small spheres, each with a mass of 20 g, are suspended from a common point by two insulating strings of length 40 cm each. The spheres are identically charged and the separation between the balls at equilibrium is found to be 4 cm. Find the charge on each sphere.
A particle with a charge of 2.0 × 10−4 C is placed directly below and at a separation of 10 cm from the bob of a simple pendulum at rest. The mass of the bob is 100 g. What charge should the bob be given so that the string becomes loose?
Two identically-charged particles are fastened to the two ends of a spring of spring constant 100 N m−1 and natural length 10 cm. The system rests on a smooth horizontal table. If the charge on each particle is 2.0 × 10−8 C, find the extension in the length of the spring. Assume that the extension is small as compared to the natural length. Justify this assumption after you solve the problem.
Two equal charges, 2.0 × 10−7 C each, are held fixed at a separation of 20 cm. A third charge of equal magnitude is placed midway between the two charges. It is now moved to a point 20 cm from both the charges. How much work is done by the electric field during the process?
How much work has to be done in assembling three charged particles at the vertices of an equilateral triangle, as shown in the figure?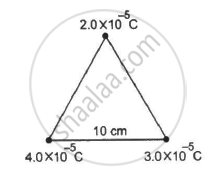
Two identical particles, each with a charge of 2.0 × 10−4 C and mass of 10 g, are kept at a separation of 10 cm and then released. What would be the speed of the particles when the separation becomes large?
Define a unit charge.
Answer the following question.
What is relative permittivity?
Explain in detail Coulomb’s law and its various aspects.
Three charges +Q, q, +Q are placed respectively, at distance, 0, d/2 and d from the origin, on the X-axis. If the net force experienced by +Q, placed at x = 0, is zero then value of q is ____________.
For charges q1 and q2 separated by a distance R the magnitude of the electrostatic force is given by ______.
The unit of charge is ______.
Electric charge of any system is ______.
Two charges q and – 3q are placed fixed on x-axis separated by distance ‘d’. Where should a third charge 2q be placed such that it will not experience any force?
