Advertisements
Advertisements
प्रश्न
Two pendulums with identical bobs and lengths are suspended from a common support such that in rest position the two bobs are in contact (Figure). One of the bobs is released after being displaced by 10° so that it collides elastically head-on with the other bob.
- Describe the motion of two bobs.
- Draw a graph showing variation in energy of either pendulum with time, for 0 ≤ t ≤ 2T, where T is the period of each pendulum.
Advertisements
उत्तर
a. Consider the adjacent diagram in which the bob B is displaced through an angle θ and released.
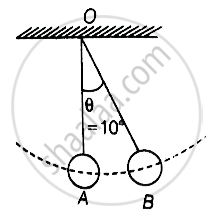
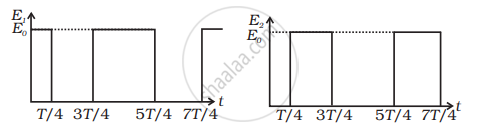
At t = 0, suppose bob B is displaced by θ = 10° to the right. It is given potential energy E1 = E. Energy of A, E2 = 0
When B is released, it strikes A at t = T/4. In the head-on elastic collision between B and A comes to rest and A gets the velocity of B. Therefore. E1 = 0 and E2 = E. At t = 27T/4, B reaches its extreme right position when KE of A is converted into PE = E2 = E. Energy of B, E1 = 0.
At t = 3T/4, A reaches its mean position. when its PE is converted into KE = E2 = E. It collides elastically with B and transfers the whole of its energy to B. Thus, E2 = 0 and E1 = E. The entire process is repeated.
b. The values of energies of B and A at different time intervals are tabulated here. The plot of energy with time 0 ≤ t ≤ 2T is shown separately for 8 and A in the figure below.
| Time (t) | Energy of A (E1) |
Energy of B (E2) |
| 0 | E | 0 |
| T/4 | 0 | E |
| 2T/4 | 0 | E |
| 3T/4 | E | 0 |
| 4T/4 | E | 0 |
| 5T/4 | 0 | E |
| 6T/4 | 0 | E |
| 7T/4 | E | 0 |
| 8T/4 | E | 0 |
APPEARS IN
संबंधित प्रश्न
State if the following statement is true or false. Give a reason for your answer.
Total energy of a system is always conserved, no matter what internal and external forces on the body are present.
Answer carefully, with reason:
Is the total linear momentum conserved during the short time of an elastic collision of two balls?
A molecule in a gas container hits a horizontal wall with speed 200 m s–1 and angle 30° with the normal, and rebounds with the same speed. Is momentum conserved in the collision? Is the collision elastic or inelastic?
Answer the following question.
Discuss the following as special cases of elastic collisions and obtain their exact or approximate final velocities in terms of their initial velocities.
- Colliding bodies are identical.
- A very heavy object collides on a lighter object, initially at rest.
- A very light object collides on a comparatively much massive object, initially at rest.
Explain the characteristics of elastic and inelastic collision.
Define the following:
Coefficient of restitution
What is inelastic collision? In which way it is different from an elastic collision. Mention a few examples in day-to-day life for inelastic collision.
In Rutherford experiment, for head-on collision of a-particles with a gold nucleus, the impact parameter is ______.
In inelastic collision, ____________.
A mass M moving with velocity 'v' along x-axis collides and sticks to another mass 2M which is moving along Y-axis with velocity 3v. After collision, the velocity of the combination is ______.
A particle of mass 'm' collides with another stationary particle of mass 'M'. A particle of mass 'm' stops just after collision. The coefficient of restitution is ______.
A smooth sphere of mass 'M' moving with velocity 'u' directly collides elastically with another sphere of mass 'm' at rest. After collision, their final velocities are V' and V respectively. The value of V is given by ______.
During inelastic collision between two bodies, which of the following quantities always remain conserved?
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V as shown in figure.
If the collision is elastic, which of the following (Figure) is a possible result after collision?
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1 m, calculate
- the height to which bob A will rise after collision.
- the speed with which bob B starts moving. Neglect the size of the bobs and assume the collision to be elastic.
A particle of mass m with an initial velocity u`hat"i"` collides perfectly elastically with a mass 3m at rest. It moves with a velocity v`hat"j"` after collision, then, v is given by :
A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and required 1 s to cover. How long the drunkard takes to fall in a pit 13 m away from the start?
A bag of sand of mass 9.8 kg is suspended by a rope. A bullet of 200 g travelling with speed 10 ms-1 gets embedded in it, then loss of kinetic energy will be ______.
The dimension of mutual inductance is ______.
