Advertisements
Advertisements
प्रश्न
Water is dripping out from a conical funnel of semi-vertical angle `pi/4` at the uniform rate of 2cm2/sec in the surface area, through a tiny hole at the vertex of the bottom. When the slant height of cone is 4 cm, find the rate of decrease of the slant height of water.
उत्तर
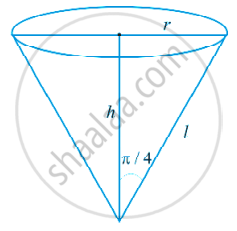
If s represents the surface area, then `"ds"/"dt" = (2"cm"^2)/sec`
s = π r.l
= `pi"l" . sin pi/4 "l"`
= `pi/sqrt(2) "l"^2`
Therefore, `"ds"/"dt" = (2pi)/sqrt(2) "l" . "dl"/"dt"`
= `sqrt(2)pi"l" * "dl"/"dt"`
When l = 4cm
`"dl"/"dt" = 1/(sqrt(2)pi4)*2`
= `1/(2sqrt(2)pi)`
= `sqrt(2)/(4pi) "cm"/"s"`
APPEARS IN
संबंधित प्रश्न
If y = f (u) is a differential function of u and u = g(x) is a differential function of x, then prove that y = f [g(x)] is a differential function of x and `dy/dx=dy/(du) xx (du)/dx`
An edge of a variable cube is increasing at the rate of 3 cm/s. How fast is the volume of the cube increasing when the edge is 10 cm long?
The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of (a) the perimeter, and (b) the area of the rectangle.
The radius of an air bubble is increasing at the rate `1/2` cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?
The total revenue in rupees received from the sale of x units of a product is given by R(x) = 13x2 + 26x + 15. Find the marginal revenue when x = 7.
The total cost C (x) associated with the production of x units of an item is given by C (x) = 0.007x3 − 0.003x2 + 15x + 4000. Find the marginal cost when 17 units are produced ?
A man 2 metres high walks at a uniform speed of 6 km/h away from a lamp-post 6 metres high. Find the rate at which the length of his shadow increases ?
The radius of a cylinder is increasing at the rate 2 cm/sec. and its altitude is decreasing at the rate of 3 cm/sec. Find the rate of change of volume when radius is 3 cm and altitude 5 cm.
A circular disc of radius 3 cm is being heated. Due to expansion, its radius increases at the rate of 0.05 cm/sec. Find the rate at which its area is increasing when radius is 3.2 cm.
The sides of an equilateral triangle are increasing at the rate of 2 cm/sec. How far is the area increasing when the side is 10 cms?
The side of a square is increasing at the rate of 0.1 cm/sec. Find the rate of increase of its perimeter ?
The radius of a circle is increasing at the rate of 0.5 cm/sec. Find the rate of increase of its circumference ?
A cylindrical vessel of radius 0.5 m is filled with oil at the rate of 0.25 π m3/minute. The rate at which the surface of the oil is rising, is
The distance moved by the particle in time t is given by x = t3 − 12t2 + 6t + 8. At the instant when its acceleration is zero, the velocity is
For what values of x is the rate of increase of x3 − 5x2 + 5x + 8 is twice the rate of increase of x ?
The radius of a sphere is increasing at the rate of 0.2 cm/sec. The rate at which the volume of the sphere increase when radius is 15 cm, is
The radius of a circular plate is increasing at the rate of 0.01 cm/sec. The rate of increase of its area when the radius is 12 cm, is
In a sphere the rate of change of surface area is
The sides of an equilateral triangle are increasing at the rate of 2 cm/sec. The rate at which the area increases, when side is 10 cm is ______.
If the rate of change of the area of the circle is equal to the rate of change of its diameter then its radius is equal to ____________.
If the rate of change of volume of a sphere is equal to the rate of change of its radius then the surface area of a sphere is ____________.
A cylindrical tank of radius 10 feet is being filled with wheat at the rate of 3/4 cubic feet per minute. The then depth of the wheat is increasing at the rate of
A man 1.6 m tall walks at the rate of 0.3 m/sec away from a street light that is 4 m above the ground. At what rate is the tip of his shadow moving? At what rate is his shadow lengthening?
If equal sides of an isosceles triangle with fixed base 10 cm are increasing at the rate of 4 cm/sec, how fast is the area of triangle increasing at an instant when all sides become equal?
An edge of a variable cube is increasing at the rate of 10 cm/sec. How fast will the volume of the cube increase if the edge is 5 cm long?
Given that `1/y + 1/x = 1/12` and y decreases at a rate of 1 cms–1, find the rate of change of x when x = 5 cm and y = 1 cm.
