Advertisements
Advertisements
Question
Water is dripping out from a conical funnel of semi-vertical angle `pi/4` at the uniform rate of 2cm2/sec in the surface area, through a tiny hole at the vertex of the bottom. When the slant height of cone is 4 cm, find the rate of decrease of the slant height of water.
Solution
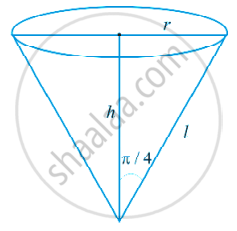
If s represents the surface area, then `"ds"/"dt" = (2"cm"^2)/sec`
s = π r.l
= `pi"l" . sin pi/4 "l"`
= `pi/sqrt(2) "l"^2`
Therefore, `"ds"/"dt" = (2pi)/sqrt(2) "l" . "dl"/"dt"`
= `sqrt(2)pi"l" * "dl"/"dt"`
When l = 4cm
`"dl"/"dt" = 1/(sqrt(2)pi4)*2`
= `1/(2sqrt(2)pi)`
= `sqrt(2)/(4pi) "cm"/"s"`
APPEARS IN
RELATED QUESTIONS
A point source of light is hung 30 feet directly above a straight horizontal path on which a man of 6 feet in height is walking. How fast will the man’s shadow lengthen and how fast will the tip of shadow move when he is walking away from the light at the rate of 100 ft/min.
The radius of a circle is increasing uniformly at the rate of 3 cm/s. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
An edge of a variable cube is increasing at the rate of 3 cm/s. How fast is the volume of the cube increasing when the edge is 10 cm long?
The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base?
The volume of a sphere is increasing at the rate of 8 cm3/s. Find the rate at which its surface area is increasing when the radius of the sphere is 12 cm.
Find the rate of change of the total surface area of a cylinder of radius r and height h, when the radius varies?
Find the rate of change of the volume of a ball with respect to its radius r. How fast is the volume changing with respect to the radius when the radius is 2 cm?
The radius of a spherical soap bubble is increasing at the rate of 0.2 cm/sec. Find the rate of increase of its surface area, when the radius is 7 cm.
A stone is dropped into a quiet lake and waves move in circles at a speed of 4 cm/sec. At the instant when the radius of the circular wave is 10 cm, how fast is the enclosed area increasing?
A man 180 cm tall walks at a rate of 2 m/sec. away, from a source of light that is 9 m above the ground. How fast is the length of his shadow increasing when he is 3 m away from the base of light?
A ladder 13 m long leans against a wall. The foot of the ladder is pulled along the ground away from the wall, at the rate of 1.5 m/sec. How fast is the angle θ between the ladder and the ground is changing when the foot of the ladder is 12 m away from the wall.
A balloon in the form of a right circular cone surmounted by a hemisphere, having a diameter equal to the height of the cone, is being inflated. How fast is its volume changing with respect to its total height h, when h = 9 cm.
A man 2 metres high walks at a uniform speed of 6 km/h away from a lamp-post 6 metres high. Find the rate at which the length of his shadow increases ?
The volume of metal in a hollow sphere is constant. If the inner radius is increasing at the rate of 1 cm/sec, find the rate of increase of the outer radius when the radii are 4 cm and 8 cm respectively.
Sand is being poured onto a conical pile at the constant rate of 50 cm3/ minute such that the height of the cone is always one half of the radius of its base. How fast is the height of the pile increasing when the sand is 5 cm deep ?
A kite is 120 m high and 130 m of string is out. If the kite is moving away horizontally at the rate of 52 m/sec, find the rate at which the string is being paid out.
The radius of a circle is increasing at the rate of 0.5 cm/sec. Find the rate of increase of its circumference ?
Find the surface area of a sphere when its volume is changing at the same rate as its radius ?
The distance moved by a particle travelling in straight line in t seconds is given by s = 45t + 11t2 − t3. The time taken by the particle to come to rest is
A man 2 metres tall walks away from a lamp post 5 metres height at the rate of 4.8 km/hr. The rate of increase of the length of his shadow is
In a sphere the rate of change of volume is
A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic metre per hour. Then the depth of the wheat is increasing at the rate of
A 13 m long ladder is leaning against a wall, touching the wall at a certain height from the ground level. The bottom of the ladder is pulled away from the wall, along the ground, at the rate of 2 m/s. How fast is the height on the wall decreasing when the foot of the ladder is 5 m away from the wall?
The radius of a cylinder is increasing at the rate of 3 m/s and its height is decreasing at the rate of 4 m/s. The rate of change of volume when the radius is 4 m and height is 6 m, is ____________.
The radius of a circle is increasing uniformly at the rate of 3 cm per second. Find the rate at which the area of the circle is increasing when the radius is 10 cm.
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall?
A cylindrical tank of radius 10 feet is being filled with wheat at the rate of 3/4 cubic feet per minute. The then depth of the wheat is increasing at the rate of
A particle moves along the curve 3y = ax3 + 1 such that at a point with x-coordinate 1, y-coordinate is changing twice as fast at x-coordinate. Find the value of a.
