Question

ΔXYZ असा काढा, की ∠Y = 58°, ∠X = 46° आणि त्रिकोणाची परिमिती 10.5 सेमी असेल.

Answer 1

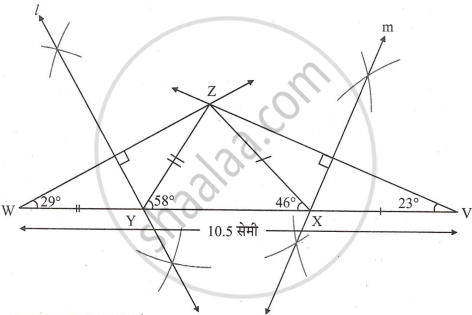
कच्ची आकृती:

स्पष्टीकरण:

(i) आकृतीत दाखवल्याप्रमाणे, YX रेषेवर W आणि V बिंदू घ्या, जसे की

YW = ZY and XV = ZX     ...(i)

YW + YX + XV = WV     ...[W-Y-X, Y-X-V]

∠Y + YX + ∠X = WV      ...(ii) [(i) पासून]

तसेच,

∠Y + YX + ∠X = 10.5 cm    ...(iii) [दिलेले]

∴ WV = 10.5 cm    ...[(ii) and (iii) पासून]

(ii) ∆ZWY मध्ये,

∠Y = YM     ...[(i) पासून]

∴ ∠YZW = ∠YWZ = x°     ...(iv) [समद्विभुज त्रिकोण प्रमेय]

∆ZYW मध्ये, ∠ZYX हा बाह्य कोन आहे.

∴ ∠YZW + ∠YWZ = ∠ZYX     ...[दूरस्थ आतील कोन प्रमेय]

∴ x + x = 58°    ...[(iv) पासून]

∴ 2x = 58°

∴ x = 29°

∴ ∠ZWY = 29°

∴ ∠W = 29°

∴ त्याचप्रमाणे, ∠V = 23°

(iii) आता, ∆ZWV मध्ये

∠W = 29°, ∠V = 23° आणि

WV= 10.5 सेमी

म्हणून, ∆ZWV काढता येतो.

(iv) ZY = YW

∴ बिंदू Y हा रेख ZW च्या लंबदुभाजकावर आहे.

तसेच, ZX = XV

∴ बिंदू X हा रेख ZV च्या लंबदुभाजकावर आहे.

∴ बिंदू Y आणि X अनुक्रमे ZW आणि ZV चे लंबदुभाजक रेखाटून शोधता येतात.

∴ ∆XYZ काढता येतो.

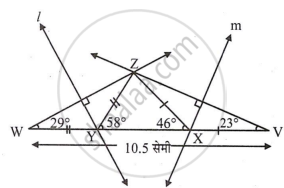
रचनेच्या पायऱ्या:

1. रेख AB हा 10.5 सेमी लांबीचा रेषाखंड काढा.
2. बिंदू A पाशी 23° मापाचा कोन करणारा किरण काढा.
3. बिंदू B पाशी 29° मापाचा कोन करणारा किरण काढा.
4. दोन्ही किरणांच्या छेदनबिंदूला Z हे नाव द्या.
5. रेख ZA व रेख ZB चे लंबदुभाजक काढा. ते रेषा AB ला ज्या बिंदूंत छेदतील त्यांना अनुक्रमे X आणि Y ही नावे द्या.
6. रेख ZX आणि रेख ZY काढा.

ΔXYZ हा अपेक्षित त्रिकोण आहे.