Question

ΔLMN असा काढा, की ∠M = 60°, ∠N = 80° आणि LM + MN + NL = 11 सेमी.

Answer 1

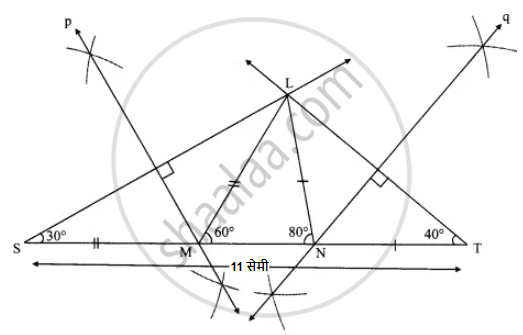
कच्ची आकृती:

स्पष्टीकरण:

(i) आकृतीत दाखवल्याप्रमाणे, MN वर बिंदू S आणि T घ्या, जसे की

MS = LM आणि NT = LN    ...(i)

MS + MN + NT = ST      ...[S-M-N, M-N-T]

∴ LM + MN + LN = ST    ...(ii)

तसेच,

LM + MN + LN = 11 cm     ...(iii)

∴ ST = 11 सेमी       ...[(ii) आणि (iii) पासून]

(ii) ∆LSM मध्ये

LM = MS

∴ ∠MLS = ∠MSL = x°      ...(iv) [समद्विभुज त्रिकोण प्रमेय]

∆LMS मध्ये, ∠LMN हा बाह्य कोन आहे.

∴ ∠MLS + ∠MSL = ∠LMN     ...[दूरस्थ आतील कोन प्रमेय]

∴ x + x = 60°     ...[(iv) पासून]

∴ 2x = 60°

∴ x = 30°

∴ ∠LSM = 30°

∴ ∠S = 30°

त्याचप्रमाणे, ∠T = 40°

(iii) आता, ∆LST मध्ये

∠S = 30°, ∠T = 40° आणि ST = 11 सेमी

म्हणून, ALST काढता येतो.

(iv) LM = MS

∴ ∴ बिंदू M रेख LS च्या लंबदुभाजकावर आहे.

तसेच LN = NT

∴ बिंदू N हा रेख LT च्या लंबदुभाजकावर आहे.

∴ बिंदू M आणि N अनुक्रमे LS आणि LT चे लंबदुभाजक रेखाटून शोधता येतात.

∴ ∆LMN काढता येतो.

रचनेच्या पायऱ्या:

1. रेख ST हा 11 सेमी लांबीचा रेषाखंड काढा.
2. बिंदू S पाशी 30° मापाचा कोन करणारा किरण काढा.
3. बिंदू T पाशी 40° मापाचा कोन करणारा किरण काढा.
4. दोन्ही किरणांच्या छेदनबिंदूला L हे नाव द्या.
5. रेख LS व रेख LT चे लंबदुभाजक काढा. ते रेषा ST ला ज्या बिंदूंत छेदतील त्यांना अनुक्रमे M आणि N ही नावे द्या.
6. रेख LM आणि रेख LN काढा.

ΔLMN हा अपेक्षित त्रिकोण आहे.