Question

ΔXYZ की रचना कीजिए जिसमें YZ = 7.4 सेमी । m`angle`XYZ = 45° तथा XY - XZ = 2.7 सेमी।

Answer 1

कच्ची आकृति:

स्पष्टीकरण:

XY - XZ = 2.7 सेमी ∴ XY > XZ

रेखाखंड YZ खींचे। रेख YZ से 45° का कोण बनाने वाली किरण YL खींचिए।

इस किरण पर बिंदु X प्राप्त करने के लिए किरण YL पर बिंदु W इस

प्रकार लिया कि YW = 2.7 सेमी तथा XY = XW + YW ....[X-W-Y]

∴ XY = XW + 2.7 ....(`because` YW = 2.7 सेमी)

∴ XY - XW = 2.7 सेमी ....(1)

अब, XY - XZ = 2.7 सेमी ....(2)

∴ XY - XW = XY - XZ ....[(i) और (ii) से]

∴ XW = XZ

∴ X बिंदु रेख WZ के लंबसमद्‌विभाजक पर है।

∴ बिंदु X किरण YL तथा रेख WZ के लंबसमद्‌विभाजक का प्रतिच्छेदन बिंदु है।

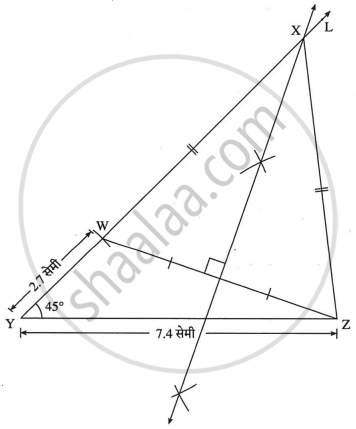
रचना के सोपान

1. 7.4 सेमी लंबाईवाला रेख YZ खींचिए।
2. बिंदु Y से 45° का कोण बनाने वाली किरण YL खींचिए।
3. किरण YL पर बिंदु W इस प्रकार लीजिए कि YW = 2.7 सेमी।
4. रेख WZ खींचकर उसका लंब समद्‌विभाजक खींचिए।
5. किरण YL को रेख WZ का लंबसमद्‌विभाजक जिस स्थान पर प्रतिच्छेदित करता है, उसे X नाम दीजिए।
6. रेख XZ खींचिए।

ΔXYZ यह अभीष्ट त्रिभुज है।