Advertisements
Advertisements
प्रश्न
ΔXYZ मे XY = 4 सेमी, YZ = 6 सेमी, XZ = 5 सेमी, यदि ΔXYZ ~ ΔPQR तथा PQ = 8 सेमी हो तो ΔPQR की शेष भुजाओं की लंबाई ज्ञात कीजिए।
उत्तर
Δ XYZ ~ Δ PQR
∴` ("XY")/("PQ") = ("YZ")/("QR") = ("XZ")/("PR")` ...[समरूप त्रिभुज के संगत भुजाएँ]
∴ `4/8 = 6/("QR") = 5/("PR")`
∴`4/8 = 6/("QR")`
∴ QR × 4 = 8 × 6
∴ QR = `(8 xx6)/4`
∴ QR = 12 सेमी
`4/8 = 5/("PR")`
∴ 4 × PR = 8 × 5
∴ PR = `(8 xx5)/4`
PR = 10 सेमी
भुजा QR = 12 सेमी, भुजा PR = 10 सेमी
APPEARS IN
संबंधित प्रश्न
आकृति में, DE || BC है। EC ज्ञात कीजिए:
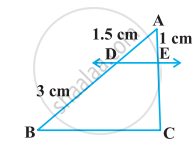
आकृति में यदि LM || CB और LN || CD हो तो सिद्ध कीजिए कि `"AM"/"AB" = "AN"/"AD"` है।

आकृति में DE || AC और DF || AE है। सिद्ध कीजिए कि `"BF"/"FE" = "BE"/"EC"` है।
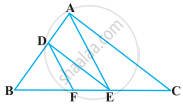
आकृति में DE || OQ और DF || OR है। दर्शाइए कि EF || QR है।
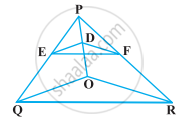
आकृति में क्रमशः OP, OQ और OR पर स्थित बिंदु A, B और C इस प्रकार हैं कि AB || PQ और AC || PR है। दर्शाइए कि BC || QR है।
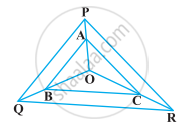
आधारभूत समानुपातिकता प्रमेय का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य-बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।(याद कीजिए कि आप इसे कक्षा IX में सिद्ध कर चुके हैं।)
एक चतुर्भुज ABCD के विकर्ण परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि `("AO")/("BO") = ("CO")/("DO")` है। दर्शाइए कि ABCD एक समलंब है।
यह दिया है कि `(BC)/(QR) = 1/3` के साथ ΔABC ~ ΔPQR, है। तब `(ar(PRQ))/(ar(BCA))` बराबर ______ है।
दो समरूप त्रिभुजों के संगत शीर्षलंबों का अनुपात `3/5` है। क्या यह कहना सही है कि इन त्रिभुजों के क्षेत्रफलों का अनपात `6/5` है? क्यों?
सिद्ध कीजिए कि यदि किसी त्रिभुज की एक भुजा के समांतर, उसकी अन्य दो भुजाओं को प्रतिच्छेद करने के लिए, रेखा खींची जाए, तो ये दोनों भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
