Advertisements
Advertisements

In the given figure, square ABCD is inscribed in the sector A - PCQ. The radius of sector C - BXD is 20 cm. Complete the following activity to find the area of shaded region
Concept: Length of an Arc
ΔDEF ~ ΔMNK. If DE = 5, MN = 6, then find the value of `"A(ΔDEF)"/"A(ΔMNK)"`
Concept: Similar Triangles
In the following figure, in Δ PQR, seg RS is the bisector of ∠PRQ.
PS = 3, SQ = 9, PR = 18. Find QR.

Concept: Similarity of Triangles
The ratio of the areas of two triangles with the common base is 14 : 9. Height of the larger triangle is 7 cm, then find the corresponding height of the smaller triangle.
Concept: Properties of Ratios of Areas of Two Triangles
In the figure given below, Ray PT is bisector of ∠QPR. If PQ = 5.6 cm, QT = 4 cm and TR = 5 cm, find the value of x .

Concept: Similarity of Triangles
In a triangle ABC, line l || Side BC and line l intersects side AB and AC in points P and Q, respectively. Prove that: `"AP"/"BP"="AQ"/"QC"`

Concept: Similarity of Triangles
`triangleDEF ~ triangleMNK`. If DE = 5 and MN = 6, then find the value of `(A(triangleDEF))/(A(triangleMNK))`
Concept: Similarity of Triangles
The ratio of the areas of two triangles with common base is 6:5. Height of the larger triangle of 9 cm, then find the corresponding height of the smaller triangle.
Concept: Properties of Ratios of Areas of Two Triangles
In the following figure, seg DH ⊥ seg EF and seg GK ⊥ seg EF. If DH = 18 cm, GK = 30 cm and `A(triangle DEF) = 450 cm^2`, then find:
1) EF
2) `A(triangle GFE)`
3) `A(square DFGE)`

Concept: Similarity of Triangles
Base of a triangle is 9 and height is 5. Base of another triangle is 10 and height is 6. Find the ratio of areas of these triangles.
Concept: Properties of Ratios of Areas of Two Triangles
In the given figure, BC ⊥ AB, AD ⊥ AB, BC = 4, AD = 8, then find `("A"(∆"ABC"))/("A"(∆"ADB"))`
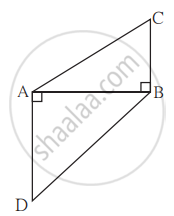
Concept: Properties of Ratios of Areas of Two Triangles
In adjoining figure, seg PS ⊥ seg RQ, seg QT ⊥ seg PR. If RQ = 6, PS = 6 and PR = 12, then Find QT.
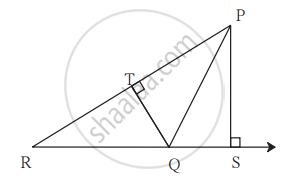
Concept: Similar Triangles
In adjoining figure, PQ ⊥ BC, AD ⊥ BC then find following ratios.
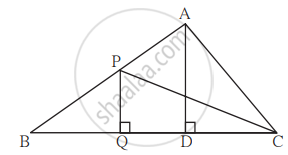
- `("A"(∆"PQB"))/("A"(∆"PBC"))`
- `("A"(∆"PBC"))/("A"(∆"ABC"))`
- `("A"(∆"ABC"))/("A"(∆"ADC"))`
- `("A"(∆"ADC"))/("A"(∆"PQC"))`
Concept: Properties of Ratios of Areas of Two Triangles
In ∆PQR, PM = 15, PQ = 25 PR = 20, NR = 8. State whether line NM is parallel to side RQ. Give reason.

Concept: Property of Three Parallel Lines and Their Transversals
In ∆MNP, NQ is a bisector of ∠N. If MN = 5, PN = 7 MQ = 2.5 then find QP.
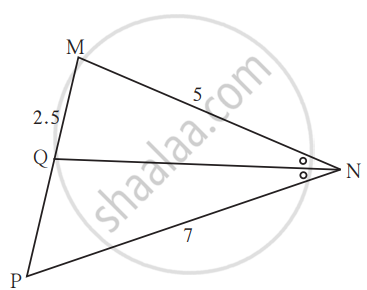
Concept: Property of an Angle Bisector of a Triangle
In trapezium ABCD, side AB || side PQ || side DC, AP = 15, PD = 12, QC = 14, Find BQ.

Concept: Property of Three Parallel Lines and Their Transversals
In the given figure, if AB || CD || FE then find x and AE.

Concept: Property of an Angle Bisector of a Triangle
Are the triangles in the given figure similar? If yes, by which test?

Concept: Similarity of Triangles
In trapezium PQRS, side PQ || side SR, AR = 5AP, AS = 5AQ then prove that, SR = 5PQ
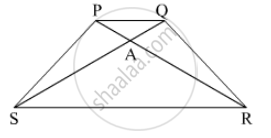
Concept: Properties of Ratios of Areas of Two Triangles
If ∆ABC ~ ∆PQR, A (∆ABC) = 80, A (∆PQR) = 125, then fill in the blanks. \[\frac{A\left( ∆ ABC \right)}{A\left( ∆ . . . . \right)} = \frac{80}{125} \therefore \frac{AB}{PQ} = \frac{......}{......}\]
Concept: Areas of Similar Triangles
