Advertisements
Advertisements
Question
1 + 3 + 5 + ......... + 101 या 1 ते 101 पर्यंत विषम नैसर्गिक संख्यांची बेरीज करा.
Solution
1 ते 101 पर्यंतच्या विषम संख्या:
1, 3, 5, …, 101
वरील क्रमिका अंकगणिती श्रेढी आहे.
∴ a = 1, d = 3 – 1 = 2
अंकगणिती श्रेढीतील पदांची संख्या n मानू.
तर, , tn = 101
परंतु, tn = a + (n – 1)d,
101 = 1 + (n – 1) (2)
∴ 101 = 1 + 2n – 2
∴ 101 = 2n – 1
∴ 102 = 2n
∴ n = `102/2 = 51`
आता, Sn = `"n"/2` (t1 + tn)
∴ S51 = `51/2`(1 + 101)
= `51/2(102)`
= 51 × 51
= 2601
∴ 1 ते 101 पर्यंतच्या विषम संख्यांची बेरीज 2601 आहे.
APPEARS IN
RELATED QUESTIONS
एका अंकगणिती श्रेढीचे पहिले पद 6 व सामान्य फरक 3 आहे तर S27 काढा.
a = 6, d = 3, S27 = ?
`"S"_"n" = "n"/2 [square + ("n" - 1)"d"]`
`"S"_27 = 27/2 [12 + (27 - 1)square]`
`= 27/2 xx square`
= 27 × 45 = `square`
पहिल्या 123 सम नैसर्गिक संख्यांची बेरीज काढा.
एका अंकगणिती श्रेढीचे 19 वे पद 52 आणि 38 वे पद 128 आहे, तर तिच्या पहिल्या 56 पदांची बेरीज काढा.
1 व 140 यांच्या दरम्यान, 4 ने भाग जाणाऱ्या नैसर्गिक संख्यांची बेरीज किती आहे, हे काढण्यासाठी खालील कृती पूर्ण करा.
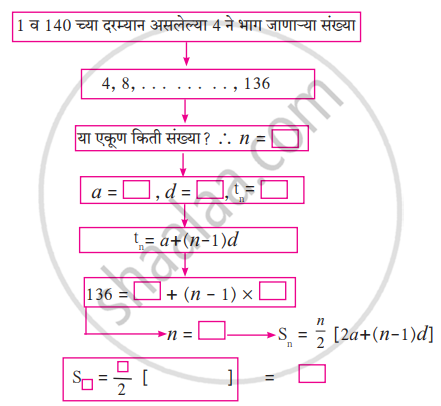
1 व 140 यांच्या दरम्यान 4 ने भाग जाणाऱ्या संख्यांची बेरीज = `square`
एका अंकगणिती श्रेढीतील चार क्रमागत पदांची बेरीज 12 आहे. तसेच, त्या चार क्रमागत पदांपैकी तिसऱ्या व चौथ्या पदांची बेरीज 14 आहे, तर ती चार पदे काढा.
(चार क्रमागत पदे a - d, a, a + d, a + 2d माना.)
ज्या अंकगणिती श्रेढीचे पहिले पद a आहे. दुसरे पद b आहे आणि शेवटचे पद c आहे, तर त्या श्रेढीतील सर्व पदांची बेरीज `((a + c)(b + c - 2a))/(2(b - a))` एवढी आहे हे दाखवा.
पहिल्या 1000 धन पूर्णांकांची बेरीज करा.
कृती: समजा, 1 + 2 + 3 + .........+ 1000
अंकगणिती श्रेढीच्या पहिल्या n पदांच्या बेरजेचे सूत्र Sn = `square` वापरून,
S1000 = `square/2` (1 + 1000)
= 500 × 1001
= `square`
प्रथम 1000 धन पूर्णांकांची बेरीज `square` एवढी आहे.
12, 14, 16, 18, 20, ......... या अंकगणिती श्रेढीच्या पहिल्या 100 पदांची बेरीज करा.
कृती: येथे, a = 12, d = `square` n = 100, S100 = ?
Sn = `"n"/2[square + ("n" - 1)"d"]`
S100 = `square/2`[24 + (100 – 1)d]
= 50 (24 + `square`)
= `square`
= `square`
मनीष आणि सविता यांच्या आजच्या वयांची बेरीज 31 वर्षे आहे. 3 वर्षांपूर्वी मनीषचे वय सविताच्या त्यावेळच्या वयाच्या चौपट होते, तर त्या दोघांची आजची वये काढा.
त्रिकोणाच्या तीन कोनांची मापे अंकगणिती श्रेढरीमध्ये आहेत. सर्वांत लहान कोनाचे माप साधारण फरकाच्या पाचपट आहे, तर त्या त्रिकोणाच्या तीनही कोनांची मापे काढा. (त्रिकोणाच्या कोनांची मापे a, a + d, a + 2d घ्या.)
