Advertisements
Advertisements
Question
34.05 mL of phosphorus vapour weighs 0.0625 g at 546 °C and 0.1 bar pressure. What is the molar mass of phosphorus?
Solution 1
Given,
p = 0.1 bar
V = 34.05 mL = 34.05 × 10–3 L = 34.05 × 10–3 dm3
R = 0.083 bar dm3 K–1 mol–1
T = 546°C = (546 + 273) K = 819 K
The number of moles (n) can be calculated using the ideal gas equation as:
`"pV" = "nRT"`
`=> "n" = ("pV")/("RT")`
`= (0.1 xx 34.05 xx 10^(-3))/(0.083 xx 819)`
`= 5.01 xx 10^(-5)` mol
Therefore, molar mass of phosphorus = `(0.0625)/(5.01 xx 10^(-5)) = 1247.5 " g mol"^(-1)`
Hence, the molar mass of phosphorus is 1247.5 g mol–1.
Solution 2
Calculation of volume at `0^@" C"` and 1 bar pressure
`("P"_1"V"_1)/"T"_1 = ("P"_2"V"_2)/"T"_2` i.e
`(1xx34.05)/(546 + 273) = (1xx "V"_2)/273 or "V"_2 = 11.35 " ml"`
11.35 mL of vapour at 0°C and 1 bar pressure weight = 0.0625 g
∴ 22700 mL of vapour at 0°C and 1 bar pressure will weigh
`= 0.0625/11.35 xx 22700 = 125" g"`
∴ Molar mass = `125 " g mol"^(-1)`
Alternatively using
R = 0.083 bar `" dm"^3 "K"^(-1) "mol"^(-1)`
PV = nRT, i.e
`"n"= ("PV")/("RT") - (1.0 " bar" xx(34.05 xx 10^(-3) " dm"^(3)))/(0.003 " bar" " dm"^(3) "K"^(-1) "Mol"^(-1) xx 819 "K")`
`= 5 xx 10^(-4) " mol"`
∴ Mass of 1 mole = `0.0625/(5 xx 10^(-4))" g" = 125 " g"`
∴ `"Molar mass" = 125 " g mol"^(-1)`
APPEARS IN
RELATED QUESTIONS
Calculate the temperature of 4.0 mol of a gas occupying 5 dm3 at 3.32 bar.
(R = 0.083 bar dm3 K–1 mol–1).
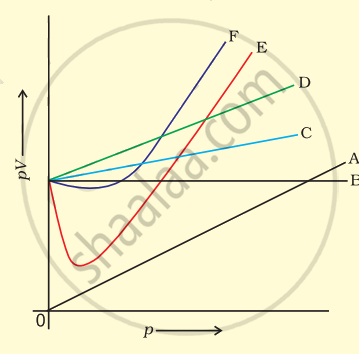
Which curve in figure represents the curve of ideal gas?
The relation between pressure exerted by an ideal gas (Pideal) and observed pressure (Preal) is given by the equation
Pideal = Preal + `(an^2)/V^2`
If pressure is taken in Nm–2, number of moles in mol and volume in m3, Calculate the unit of ‘a’. What will be the unit of ‘a’ when pressure is in atmosphere and volume in dm3?
