Advertisements
Advertisements
Question
A student forgot to add the reaction mixture to the round-bottomed flask at 27 °C but instead, he/she placed the flask on the flame. After a lapse of time, he realized his mistake and using a pyrometer he found the temperature of the flask was 477 °C. What fraction of air would have been expelled out?
Solution
Let the volume of the round bottomed flask be V.
Then, the volume of air inside the flask at 27° C is V.
Now,
V1 = V
T1 = 27°C = 300 K
V2 =?
T2 = 477° C = 750 K
According to Charles’s law,
`"V"_1/"T"_1 = "V"_2/"T"_2`
`=> "V"_2 = ("V"_1"T"_2)/"T"_1`
`= (750" V")/300`
= 2.5 V
Therefore, volume of air expelled out = 2.5 V - V = 1.5 V
Hence, fraction of air expelled out = `(1.5 " V")/(2.5 " V") = 3/5`
APPEARS IN
RELATED QUESTIONS
In terms of Charles’ law explain why - 273°C is the lowest possible temperature.
The variation of pressure with volume of the gas at different temperatures can be graphically represented as shown in figure.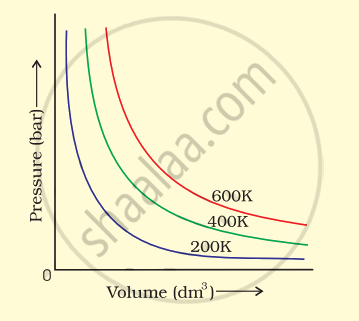
On the basis of this graph answer the following questions.
(i) How will the volume of a gas change if its pressure is increased at constant temperature?
(ii) At a constant pressure, how will the volume of a gas change if the temperature is increased from 200 K to 400 K?
Match the following gas laws with the equation representing them.
| (i) Boyle's law | (a) `V oo n` at constant T and p |
| (ii) Charle's law | (b) PTotal = p1 + p2 + p3 + at constant T, V |
| (iii) Dalton's law | (c) `(pV)/T` = Constant T |
| (iv) Avogadro law | (d) `V oo T` at constant n and p |
| (e) `P oo 1/V` at constant n and T |
If V0 is the volume of a given mass of gas at 273 K at a constant pressure then according to Charle's law, the volume at 10°C will be:
