Advertisements
Advertisements
Question
A barometer correctly reads the atmospheric pressure as 76 cm of mercury. Water droplets are slowly introduced into the barometer tube by a dropper. The height of the mercury column first decreases and then becomes constant. If the saturation vapour pressure at the atmospheric temperature is 0.80 cm of mercury, find the height of the mercury column when it reaches its minimum value.
Solution
Atmospheric pressure = 76 cm Hg
SVP = 0.80 cm Hg
When water is introduced into the barometer, water evaporates.
Thus, it exerts its vapour pressure over the mercury meniscus.
As more and more water evaporates, the vapour pressure increases that forces down the mercury level further.
Finally, when the volume is saturated with the vapour at the atmospheric temperature, the highest vapour pressure, i.e. SVP is observed and the fall of mercury level reaches its minimum. Thus,
Net pressure acting on the column = 76 - 0.80 cmHg
Net length of Hg column at SVG = 75.2 cm
APPEARS IN
RELATED QUESTIONS
From a certain apparatus, the diffusion rate of hydrogen has an average value of 28.7 cm3 s–1. The diffusion of another gas under the same conditions is measured to have an average rate of 7.2 cm3 s–1. Identify the gas
[Hint: Use Graham’s law of diffusion: R1/R2 = (M2/M1)1/2, where R1, R2 are diffusion rates of gases 1 and 2, and M1 and M2 their respective molecular masses. The law is a simple consequence of kinetic theory.]
While gas from a cooking gas cylinder is used, the pressure does not fall appreciably till the last few minutes. Why?
A gas is kept in a rigid cubical container. If a load of 10 kg is put on the top of the container, does the pressure increase?
If it were possible for a gas in a container to reach the temperature 0 K, its pressure would be zero. Would the molecules not collide with the walls? Would they not transfer momentum to the walls?
Explain why cooking is faster in a pressure cooker.
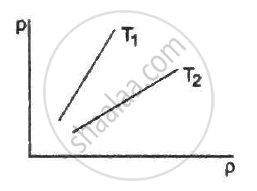
Figure shows graphs of pressure vs density for an ideal gas at two temperatures T1 and T2.
2 g of hydrogen is sealed in a vessel of volume 0.02 m3 and is maintained at 300 K. Calculate the pressure in the vessel.
Use R=8.3J K-1 mol-1
Air is pumped into an automobile tyre's tube up to a pressure of 200 kPa in the morning when the air temperature is 20°C. During the day the temperature rises to 40°C and the tube expands by 2%. Calculate the pressure of the air in the tube at this temperature.
An air bubble of radius 2.0 mm is formed at the bottom of a 3.3 m deep river. Calculate the radius of the bubble as it comes to the surface. Atmospheric pressure = 1.0 × 105 Pa and density of water = 1000 kg m−3.
A container of volume 50 cc contains air (mean molecular weight = 28.8 g) and is open to atmosphere where the pressure is 100 kPa. The container is kept in a bath containing melting ice (0°C). (a) Find the mass of the air in the container when thermal equilibrium is reached. (b) The container is now placed in another bath containing boiling water (100°C). Find the mass of air in the container. (c) The container is now closed and placed in the melting-ice bath. Find the pressure of the air when thermal equilibrium is reached.
Use R = 8.3 J K-1 mol-1
An ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area 10 cm2 and weight 1 kg. The length of the gas column in the vessel is 20 cm. The atmospheric pressure is 100 kPa. The vessel is now taken into a spaceship revolving round the earth as a satellite. The air pressure in the spaceship is maintained at 100 kPa. Find the length of the gas column in the cylinder.
Use R = 8.3 J K-1 mol-1
A gas is enclosed in a cylindrical can fitted with a piston. The walls of the can and the piston are adiabatic. The initial pressure, volume and temperature of the gas are 100 kPa, 400 cm3 and 300 K, respectively. The ratio of the specific heat capacities of the gas, Cp / Cv = 1.5. Find the pressure and the temperature of the gas if it is (a) suddenly compressed (b) slowly compressed to 100 cm3.
The initial pressure and volume of a given mass of a gas (Cp/Cv = γ) are p0 and V0. The gas can exchange heat with the surrounding. (a) It is slowly compressed to a volume V0/2 and then suddenly compressed to V0/4. Find the final pressure. (b) If the gas is suddenly compressed from the volume V0 to V0/2 and then slowly compressed to V0/4, what will be the final pressure?
On a winter day, the outside temperature is 0°C and relative humidity 40%. The air from outside comes into a room and is heated to 20°C. What is the relative humidity in the room? The saturation vapour pressure at 0°C is 4.6 mm of mercury and at 20°C it is 18 mm of mercury.
A bucket full of water is placed in a room at 15°C with initial relative humidity 40%. The volume of the room is 50 m3. (a) How much water will evaporate? (b) If the room temperature is increased by 5°C, how much more water will evaporate? The saturation vapour pressure of water at 15°C and 20°C are 1.6 kPa and 2.4 kPa respectively.
Use R = 8.3 J K-1 mol-1
A cuboidal container having dimensions 2 m × 1.5 m × 0.5 m holds a mixture of 12 g of He, 36 g of Ar, and 20 g of Ne, If the container is maintained at 300 K, Find the pressure exerted by the mixture (given MHe = 4, MAr = 40, MNe = 20).
If 1022 gas molecules each of mass 10-26 kg collide with a surface (perpendicular to it) elastically per second over an area of 1 m2 with a speed of 104 m/s, the pressure exerted by the gas molecules will be of the order of ______.
