Advertisements
Advertisements
Question
A bob attached to the string oscillates back and forth. Resolve the forces acting on the bob into components. What is the acceleration experienced by the bob at an angle θ?
Advertisements
Solution
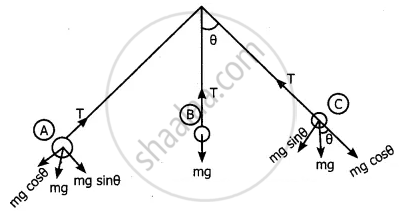
(i) Gravitational force(mg) acting downwards.
(ii) Tension (T) exerted by the string on the bob whose position determines the direction of T.
The bob is moving in a circular arc and so it has centripetal acceleration. At points, A and C bob comes to rest momentarily, and then its velocity increases when moving towards B.
Hence tangential acceleration is along the arc.
tangential acceleration = g sin θ
The gravitational force can be resolved into two components.
mg cos θ along the string
mg sin θ perpendicular to the string
At point A & C T=mg cos θ and at all other points T is greater than mg cos θ.
∴ Centripetal force = T – mg cos θ
∴ mac = T- mg cos θ
Centripetal acceleration ac = `(T - mgcostheta)/2`m
APPEARS IN
RELATED QUESTIONS
Choose the correct statement from the following.
If a person moving from pole to equator, the centrifugal force acting on him ______
What is the meaning of ‘pseudo force’?
A car takes a turn with a velocity of 50 ms-1 on the circular road of a radius of curvature of 10 m. calculate the centrifugal force experienced by a person of mass 60 kg inside the car?
Two bodies of masses 15 kg and 10 kg are connected with light string kept on a smooth surface. A horizontal force F=500 N is applied to a 15 kg as shown in the figure. Calculate the tension acting in the string?
Imagine that the gravitational force between Earth and Moon is provided by an invisible string that exists between the Moon and Earth. What is the tension that exists in this invisible string due to Earth’s centripetal force? (Mass of the Moon = 7.34 × 1022 kg, Distance between Moon and Earth = 3.84 × 108 m)
A football player kicks a 0.8 kg ball and imparts it a velocity of 12 ms-1. The contact between the foot and ball is only for one-sixtieth of a second. Find the average kicking force.
Calculate the centripetal acceleration of the Moon towards the Earth.
Explain the need for banking of tracks.
Three point masses, each of mass ‘m’ are kept at the corners of an equilateral triangle of side ‘L’. The system rotates about the center of the triangle without any change in the separation of masses during rotation. The period of rotation is directly proportional to `(cos 30° = (sqrt3)/2)` ______.
