Advertisements
Advertisements
Question
Calculate the centripetal acceleration of the Moon towards the Earth.
Advertisements
Solution
The centripetal acceleration is given by a = `v^2/r` This expression explicitly depends on Moon’s speed which is nontrivial. We can work with the formula
ω2Rm = am
am is the centripetal acceleration of the Moon due to Earth’s gravity, ω is the angular velocity
Rm is the distance between Earth and the Moon, which is 60 times the radius of the Earth.
Rm = 60R = 60 x 6.4 x 106 = 384 x 106 m
As we know the angular velocity ω = `(2π)/T` and T =
27.3 days = 27.3 x 24 x 60 x 60 second = 2.358 x 106 sec.
By substituting these values in the formula for acceleration
a6 = `((4π^2)(384×10^6))/(2.358×10^8)^2` = 0.00272 ms-2
APPEARS IN
RELATED QUESTIONS
Choose the correct statement from the following.
If a person moving from pole to equator, the centrifugal force acting on him ______
What is the meaning of ‘pseudo force’?
A car takes a turn with a velocity of 50 ms-1 on the circular road of a radius of curvature of 10 m. calculate the centrifugal force experienced by a person of mass 60 kg inside the car?
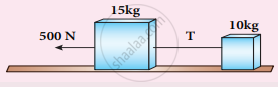
Two bodies of masses 15 kg and 10 kg are connected with light string kept on a smooth surface. A horizontal force F=500 N is applied to a 15 kg as shown in the figure. Calculate the tension acting in the string?
Imagine that the gravitational force between Earth and Moon is provided by an invisible string that exists between the Moon and Earth. What is the tension that exists in this invisible string due to Earth’s centripetal force? (Mass of the Moon = 7.34 × 1022 kg, Distance between Moon and Earth = 3.84 × 108 m)
A football player kicks a 0.8 kg ball and imparts it a velocity of 12 ms-1. The contact between the foot and ball is only for one-sixtieth of a second. Find the average kicking force.
Explain the need for banking of tracks.
Briefly explain ‘centrifugal force’ with suitable examples.
Explain the similarities and differences of centripetal and centrifugal forces.
