Advertisements
Advertisements
Question
Two masses m1 and m2 are connected with a string passing over a frictionless pulley fixed at the comer of the table as shown in the figure. The coefficient of static friction of mass m1 with the table is µs Calculate the minimum mass m3 that may be placed on m1 to prevent it from sliding. Check if m1 = 15 kg, m2 = 10 kg, m3 = 25 and µs = 0.2.
Advertisements
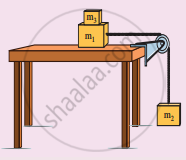
Solution
Let m3 is the mass added on m1
Maximal static friction
`f_s^max` = µsN = µs (m1 + m3)g
Here,
N = (m1 + m3)g
Tension acting on string = T = m2 g
Equate (1) and (2)
µs(m1 + m3) = m2g
µsm1 + µsm3 = m2
m3 = `f_s^max` – m1
(ii) Given,
m1 = 15 kg, m2 = 10 kg : m3 = 25 kg and µs = 0.2
m3 = `f_s^max` – m1
m3 = `10/0.2` – 15 = 50 – 15 = 35 kg
The minimum mass m3 = 35 kg has to be placed on ml to prevent it from sliding. But here m3 = 25 kg only.
The combined masses (m1 + m3) will slide.
APPEARS IN
RELATED QUESTIONS
A long stick rests on the surface. A person standing 10 m away from the stick. With what minimum speed an object of mass 0.5 kg should he has thrown so that it hits the stick. (Assume the coefficient of kinetic friction is 0.7).
People often say “For every action, there is an equivalent opposite reaction”. Here they meant ‘action of a human’. Is it correct to apply Newton’s third law to human actions? What is mean by ‘action’ in Newton's third law? Give your arguments based on Newton’s laws.
Briefly explain the origin of friction. Show that in an inclined plane, the angle of friction is equal to the angle of repose.
A uniform metal chain is placed on a rough table such that one end of the chain hangs down over the edge of the table. When two-thirds of its chain length hangs over the edge the chain start sliding. Then the coefficient of static friction is:
A block of mass m slides along a floor while a force of magnitude F is applied to it at an angle θ as shown in figure. The coefficient of kinetic friction is µK. Then, the block's acceleration 'a' is given by ______.
(g is acceleration due to gravity)
A 40 kg wooden crate is being pushed across a wooden floor with a force of 160 N. If µk = 0.3, the acceleration of the crate is ______ m/s2. (g = 10 m/s2}
A block of mass m is pulled by a constant power P placed on a rough horizontal plane. The friction co-efficient between the block and the surface is µ. Maximum velocity of the block will be:
A block of mass m = 1 kg moving on horizontal surface with speed u = 2 m/s enters a rough horizontal patch ranging from x = 0.10 m to x = 2.00 m. If the retarding force fr on the block in this range is inversely proportional to x over this range i.e.
fr = `"-k"/x` 0.10 < x < 2.00
= 0 for x < 0.10 and x > 2.00
If k = 0.5 J then the speed of this block as it crosses the patch is (use ℓn 20 = 3)
The coefficient of static friction between a car's tires and a level road is 0.80. If the car is to be stopped in a maximum time of 3.0 s, its speed cannot exceed.
There are two inclined surfaces of equal length (L) and same angle of inclination 45° with the horizontal. One of them is rough and the other is perfectly smooth. A given body takes 2 times as much time to slide down, on rough surface than on the smooth surface. The coefficient of kinetic friction (μ) between the object and the rough surface is close to ______.
