Advertisements
Advertisements
Question
A candidate is required to answer 7 questions out of 12 questions, which are divided into two groups, each containing 6 questions. He is not permitted to attempt more than 5 questions from either group. Find the number of different ways of doing question
Solution
Total number of questions = 12
Number of questions in each group = 6
7 questions are to be attempted but not more than 5 questions from either group
∴ Total number of ways = 6C5 × 6C2 × 6C4 × 6C3 + 6C3 × 6C4 + 6C2 × 6C5
= 2[6C5 × 6C2 + 6C4 × 6C3]
= `2[6 xx (6.5)/(2.1) + (6*5*4*3)/(4*3*2*1) xx (6*5*4)/(3*2*1)]`
= 2[6 × 15 + 15 × 20]
= 2[90 + 300]
= 2 × 380
= 780
Hence, the total number of ways = 780
APPEARS IN
RELATED QUESTIONS
How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that repetition of the digits is not allowed?
A Signal is generated from 2 flags by putting one flag above the other. If 4 flags of different colours are available, how many different signals can be generated?
How many numbers between 100 and 1000 have the digit 7 exactly once?
How many numbers formed with the digits 0, 1, 2, 5, 7, 8 will fall between 13 and 1000 if digits can be repeated?
A person went to a restaurant for dinner. In the menu card, the person saw 10 Indian and 7 Chinese food items. In how many ways the person can select either an Indian or a Chinese food?
Three persons enter into a conference hall in which there are 10 seats. In how many ways they can take their seats?
In how many ways 5 persons can be seated in a row?
Four children are running a race:
In how many different ways could they finish the race?
Count the number of three-digit numbers which can be formed from the digits 2, 4, 6, 8 if repetitions of digits is not allowed
How many numbers are there between 100 and 500 with the digits 0, 1, 2, 3, 4, 5? if the repetition of digits is not allowed
Count the numbers between 999 and 10000 subject to the condition that there are no restriction
To travel from a place A to place B, there are two different bus routes B1, B2, two different train routes T1, T2 and one air route A1. From place B to place C there is one bus route say B1, two different train routes say T1, T2 and one air route A1. Find the number of routes of commuting from place A to place C via place B without using similar mode of transportation
How many numbers are there between 1 and 1000 (both inclusive) which are divisible neither by 2 nor by 5?
How many strings can be formed using the letters of the word LOTUS if the word neither starts with L nor ends with S?
Find the number of ways of distributing 12 distinct prizes to 10 students?
Evaluate `("n"!)/("r"!("n" - "r")!)` when n = 6, r = 2
Evaluate `("n"!)/("r"!("n" - "r")!)` when n = 10, r = 3
Find the value of n if `1/(8!) + 1/(9!) = "n"/(10!)`
Choose the correct alternative:
The sum of the digits at the 10th place of all numbers formed with the help of 2, 4, 5, 7 taken all at a time is
Choose the correct alternative:
In an examination there are three multiple choice questions and each question has 5 choices. Number of ways in which a student can fail to get all answer correct i
Choose the correct alternative:
The number of 5 digit numbers all digits of which are odd i
How many numbers are there between 99 and 1000 having 7 in the units place?
In how many ways can this diagram be coloured subject to the following two conditions?
(i) Each of the smaller triangle is to be painted with one of three colours: red, blue or green.
(ii) No two adjacent regions have the same colour.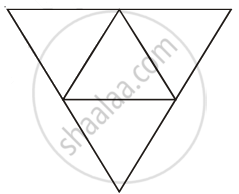
There are four bus routes between A and B; and three bus routes between B and C. A man can travel round-trip in number of ways by bus from A to C via B. If he does not want to use a bus route more than once, in how many ways can he make round trip?
In an examination there are three multiple choice questions and each question has 4 choices. Number of ways in which a student can fail to get all answer correct is ______.
Out of 18 points in a plane, no three are in the same line except five points which are collinear. Find the number of lines that can be formed joining the point
Find the number of positive integers greater than 6000 and less than 7000 which are divisible by 5, provided that no digit is to be repeated.
The number of six-digit numbers, all digits of which are odd is ______.
