Advertisements
Advertisements
Question
A circular loop of radius 9.7 cm carries a current 2.3 A. Obtain the magnitude of the magnetic field
(a) at the centre of the loop
(b) at a distance of 9.7 cm from the centre of the loop but on the axis.
Solution 1
Data: R = z = 9.7 cm = 9.7 x 10-2 m, I = 2.3 A, N = l
(a) At the centre of the coil:
The magnitude of the magnetic induction,
B = `(mu_0"NI")/(2"R")`
`= ((4pi xx 10^-7)(1)(2.3))/(2(9.7 xx 10^-2)) = (2 xx 3.142 xx 2.3)/9.7 xx 10^-5`
`= 1.49 xx 10^-5` T
(b) On the axis, at a distance z = 02 m from the coil:
B = `mu_0/(4pi) (2pi"IR"^2)/(("R"^2 + "z"^2))^(3/2)`
`("R"^2 + "z"^2)^(3/2) = (2"R"^2)^(3/2) = 2sqrt2"R"^3` (∵ R = z)
∴ B = `mu_0/(4pi) (2pi"IR"^2)/(2sqrt2"R"^3) = mu_0/(4pi) (pi"I")/(sqrt2"R")`
`= (10^-7) (3.142 xx 2.3)/(1.414 xx 9.7 xx 10^-2)`
`= 7.227/13.72 xx 10^-5 = 5.267 xx 10^-6 "T" = 5.267 mu "T"`
Solution 2
Given:
R = 9.7 cm = 9.7 × 10-2 m,
I = 2.3 A,
z = 9.7 cm = 9.7 × 10-2 m
To find:
Magnetic field
- at the centre of the loop
- on the axis at a distance
Formulae:
- Bc = `(mu_0"I")/(2"R")`
- Ba = `(mu_0"I""R"^2)/(2("z"^2 + "R"^2)^{3/2})`
Calculation:
From formula (i),
Bc = `(4pi xx 10^-7 xx 2.3)/(2 xx 9.7 xx 10^-2)`
= `(2 xx 3.142 xx 2.3)/9.7 xx 10^{-7 + 2}`
= {antilog [log 2 + log 3.142 + log 2.3 - log 9.7]} × 10-5
= {antilog (0.3010 + 0.4972 + 0.3617 - 0.9868)} × 10-5
= {antilog (0.1731)} × 10-5
= 1.489 × 10-5
≈ 1.49 × 10-5 T
= 14.9 μT
From formula (ii),
Ba = `(4pi xx 10^-7 xx 2.3 xx (9.7 xx 10^-2)^2)/(2[(9.7 xx 10^-2)^2 + (9.7 xx 10^-2)^2]^{3/2})`
= `(4pi xx 10^-7 xx 2.3 xx (9.7 xx 10^-2)^2)/(2 xx 2^{3/2} xx (9.7 xx 10^-2)^3)`
= `(pi xx 10^-7 xx 2.3)/(2^{1/2} xx (9.7 xx 10^-2))`
= `5.268 xx 10^-6`T
= 5.268 μT
- The magnetic field at the centre of 14.9 μT.
- The magnetic field on the axis at a distance of 9.7 cm from the centre is 5.268 μT.
APPEARS IN
RELATED QUESTIONS
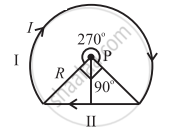
A wire loop of the form shown in the following figure carries a current I. Obtain the magnitude and direction of the magnetic field at P. (Given: `B = (mu_0I)/(4pir) sqrt2` due to
The magnetic field at the centre of a circular current carrying loop of radius 12.3 cm is 6.4 × 10-6 T. What is the magnetic moment of the loop?
The magnetic field at the centre of a circular loop of radius 12.3 cm is 6.4 x 10-6 T. What will be the magnetic moment of the loop?
A circular coil of radius R is carrying a current l1 in anti-clockwise sense. A long straight wire is carrying current l2 in the negative direction of X-axis. Both are placed in the same plane and the distance between center of coil and straight wire is d. The magnetic field at the centre of coil will be zero for the value of d equal to
The magnitude of the magnetic induction at a point on the axis at a large distance (r) from the centre of a circular coil of 'n' turns and area 'A' carrying current (l) is given by ______.
A circular coil of wire consisting of 100 turns each of radius 9 cm carries a current of 0.4 A. The magnitude of the magnetic field at the centre of coil is ______. [µ0 = 12.56 × 10-7 SI Unit]
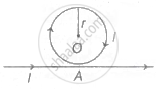
Figure show the circular coil carrying current I kept very close but not touching at a point A on a straight conductor carrying the same current l. The magnitude of magnetic induction at the centre of the circular coil will be.
How is the magnetic field of a small current loop identical to that of a short magnetic dipole? Explain.
