Advertisements
Advertisements
Question
A copper wire having resistance 0.01 ohm in each metre is used to wind a 400-turn solenoid of radius 1.0 cm and length 20 cm. Find the emf of a battery which when connected across the solenoid will cause a magnetic field of 1.0 × 10−2 T near the centre of the solenoid.
Solution
Given:
Resistance per unit length of the wire, `R/l`= 0.01 Ω/m
Radius of the wire, r = 1.0 cm = 0.01 m
Total no. of turns, N = 400
Magnetic field intensity, B = 1.0 × 10−2 T
Now,
Let E be the emf of the battery and R0 be the total resistance of the wire.
`therefore i = E / (R_0) = E /(0.01 xx 2 pi r xx 400)`
`= E/(0.01 xx 2 xx pi xx0.01 xx400)`
The magnetic field near the centre of the solenoid is given by
`B = mu_0 ni `
`= 1 xx 10^-2 = 4 pi xx 10^-7 xx 400/(20xx10^-2) xx E/(2pi xx 4 xx10^-2)`
`E = (10^-2 xx 20 xx 10^-2 xx 2 xx 10^-2)/(10^-7 xx 4 xx 10^2)`
= 1 V
APPEARS IN
RELATED QUESTIONS
Derive the expression for the magnetic field due to a solenoid of length ‘2l’, radius ‘a’ having ’n’ number of turns per unit length and carrying a steady current ‘I’ at a point
on the axial line, distance ‘r’ from the centre of the solenoid. How does this expression compare with the axial magnetic field due to a bar magnet of magnetic moment ‘m’?
Use this law to obtain the expression for the magnetic field inside an air cored toroid of average radius 'r', having 'n' turns per unit length and carrying a steady current I.
Derive an expression for the mutual inductance of two long co-axial solenoids of same length wound one over the other,
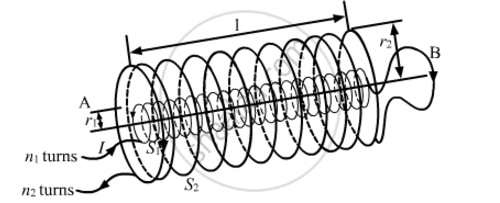
Two long coaxial insulated solenoids, S1 and S2 of equal lengths are wound one over the other as shown in the figure. A steady current "I" flow thought the inner solenoid S1 to the other end B, which is connected to the outer solenoid S2 through which the same current "I" flows in the opposite direction so as to come out at end A. If n1 and n2 are the number of turns per unit length, find the magnitude and direction of the net magnetic field at a point (i) inside on the axis and (ii) outside the combined system
Define the term self-inductance of a solenoid.
Obtain the expression for mutual inductance of a pair of long coaxial solenoids each of length l and radii r1 and r2 (r2 >> r1). Total number of turns in the two solenoids are N1 and N2, respectively.
A magnetic field of 100 G (1 G = 10−4 T) is required which is uniform in a region of linear dimension about 10 cm and area of cross-section about 10−3 m2. The maximum current-carrying capacity of a given coil of wire is 15 A and the number of turns per unit length that can be wound round a core is at most 1000 turns m−1. Suggest some appropriate design particulars of a solenoid for the required purpose. Assume the core is not ferromagnetic.
Obtain the expression for the magnetic energy stored in an inductor of self-inductance L to build up a current I through it.
Define mutual inductance between two long coaxial solenoids. Find out the expression for the mutual inductance of inner solenoid of length l having the radius r1 and the number of turns n1 per unit length due to the second outer solenoid of same length and r2 number of turns per unit length.
Draw and compare the pattern of the magnetic field lines in the two cases ?
The magnetic field inside a tightly wound, long solenoid is B = µ0 ni. It suggests that the field does not depend on the total length of the solenoid, and hence if we add more loops at the ends of a solenoid the field should not increase. Explain qualitatively why the extra-added loops do not have a considerable effect on the field inside the solenoid.
A circular coil of one turn of radius 5.0 cm is rotated about a diameter with a constant angular speed of 80 revolutions per minute. A uniform magnetic field B = 0.010 T exists in a direction perpendicular to the axis of rotation. Suppose the ends of the coil are connected to a resistance of 100 Ω. Neglecting the resistance of the coil, find the heat produced in the circuit in one minute.
A long solenoid is fabricated by closely winding a wire of radius 0.5 mm over a cylindrical nonmagnetic frame so that the successive turns nearly touch each other. What would be the magnetic field B at the centre of the solenoid if it carries a current of 5 A?
A tightly-wound, long solenoid carries a current of 2.00 A. An electron is found to execute a uniform circular motion inside the solenoid with a frequency of 1.00 × 108 rev s−1. Find the number of turns per metre in the solenoid.
A current of 1.0 A is established in a tightly wound solenoid of radius 2 cm having 1000 turns/metre. Find the magnetic energy stored in each metre of the solenoid.
A long solenoid carrying a current produces a magnetic field B along its axis. If the current is doubled and the number of turns per cm is halved, the new value of magnetic field will be equal to ______.
