Advertisements
Advertisements
Question
Define mutual inductance between two long coaxial solenoids. Find out the expression for the mutual inductance of inner solenoid of length l having the radius r1 and the number of turns n1 per unit length due to the second outer solenoid of same length and r2 number of turns per unit length.
Solution
Mutual Inductance
The ability of production of induced emf in one coil, due to varying current in the neighbouring coil is called mutual inductance.
Magnetic flux, Φ = MI Where, M is called coefficient of mutual induction
Mutual Inductance of Two Long Solenoids
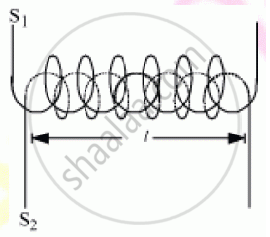
Consider two long solenoids S1 and S2 of same length l, such that solenoid S2 surrounds solenoid S1 completely.
Φ21 = M21I1
Where, M21 is the coefficient of mutual induction of the two solenoids
Magnetic field produced inside solenoid S1 on passing current through it,
B1 = μ0n1I1
Magnetic flux linked with each turn of solenoid S2 will be equal to B1 times the area of cross-section of solenoid S1.
Magnetic flux linked with each turn of the solenoid S2 = B1A
Therefore, total magnetic flux linked with the solenoid S2,
Φ21 = B1A × n2l = μ0n1I1× A× n2l
Φ21 = μ0n1n2lAI1
∴ M21 = μ0n1n2Al
Similarly, the mutual inductance between the two solenoids, when current is passed through solenoid S2 and induced emf is produced in solenoid S1, is given by
M12 = μ0n1n2Al
∴M12 = M21 = M (say)
Hence, coefficient of mutual induction between the two long solenoids
`M = mu_0n_1n_2Al`
RELATED QUESTIONS
Obtain an expression for the energy stored in a solenoid of self-inductance ‘L’ when the current through it grows from zero to ‘I’.
Derive an expression for the mutual inductance of two long co-axial solenoids of same length wound one over the other,
Define the term self-inductance of a solenoid.
Obtain the expression for mutual inductance of a pair of long coaxial solenoids each of length l and radii r1 and r2 (r2 >> r1). Total number of turns in the two solenoids are N1 and N2, respectively.
A magnetic field of 100 G (1 G = 10−4 T) is required which is uniform in a region of linear dimension about 10 cm and area of cross-section about 10−3 m2. The maximum current-carrying capacity of a given coil of wire is 15 A and the number of turns per unit length that can be wound round a core is at most 1000 turns m−1. Suggest some appropriate design particulars of a solenoid for the required purpose. Assume the core is not ferromagnetic.
The magnetic field inside a tightly wound, long solenoid is B = µ0 ni. It suggests that the field does not depend on the total length of the solenoid, and hence if we add more loops at the ends of a solenoid the field should not increase. Explain qualitatively why the extra-added loops do not have a considerable effect on the field inside the solenoid.
A long solenoid of radius 2 cm has 100 turns/cm and carries a current of 5 A. A coil of radius 1 cm having 100 turns and a total resistance of 20 Ω is placed inside the solenoid coaxially. The coil is connected to a galvanometer. If the current in the solenoid is reversed in direction, find the charge flown through the galvanometer.
A tightly-wound solenoid of radius a and length l has n turns per unit length. It carries an electric current i. Consider a length dx of the solenoid at a distance x from one end. This contains n dx turns and may be approximated as a circular current i n dx. (a) Write the magnetic field at the centre of the solenoid due to this circular current. Integrate this expression under proper limits to find the magnetic field at the centre of the solenoid. (b) verify that if l >> a, the field tends to B = µ0ni and if a >> l, the field tends to `B =(mu_0nil)/(2a)` . Interpret these results.
The length of a solenoid is 0.4 m and the number turns in it is 500. A current of 3 amp, is flowing in it. In a small coil of radius 0.01 m and number of turns 10, a current of 0.4 amp. is flowing. The torque necessary to keep the axis of this coil perpendicular to the axis of solenoid will be ______.
