Advertisements
Advertisements
प्रश्न
Define mutual inductance between two long coaxial solenoids. Find out the expression for the mutual inductance of inner solenoid of length l having the radius r1 and the number of turns n1 per unit length due to the second outer solenoid of same length and r2 number of turns per unit length.
उत्तर
Mutual Inductance
The ability of production of induced emf in one coil, due to varying current in the neighbouring coil is called mutual inductance.
Magnetic flux, Φ = MI Where, M is called coefficient of mutual induction
Mutual Inductance of Two Long Solenoids
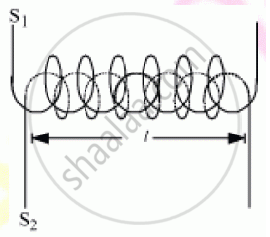
Consider two long solenoids S1 and S2 of same length l, such that solenoid S2 surrounds solenoid S1 completely.
Φ21 = M21I1
Where, M21 is the coefficient of mutual induction of the two solenoids
Magnetic field produced inside solenoid S1 on passing current through it,
B1 = μ0n1I1
Magnetic flux linked with each turn of solenoid S2 will be equal to B1 times the area of cross-section of solenoid S1.
Magnetic flux linked with each turn of the solenoid S2 = B1A
Therefore, total magnetic flux linked with the solenoid S2,
Φ21 = B1A × n2l = μ0n1I1× A× n2l
Φ21 = μ0n1n2lAI1
∴ M21 = μ0n1n2Al
Similarly, the mutual inductance between the two solenoids, when current is passed through solenoid S2 and induced emf is produced in solenoid S1, is given by
M12 = μ0n1n2Al
∴M12 = M21 = M (say)
Hence, coefficient of mutual induction between the two long solenoids
`M = mu_0n_1n_2Al`
संबंधित प्रश्न
Obtain an expression for the energy stored in a solenoid of self-inductance ‘L’ when the current through it grows from zero to ‘I’.
A closely wound solenoid 80 cm long has 5 layers of windings of 400 turns each. The diameter of the solenoid is 1.8 cm. If the current carried is 8.0 A, estimate the magnitude of B inside the solenoid near its centre.
Define self-inductance of a coil.
A wire AB is carrying a steady current of 10 A and is lying on the table. Another wire CD carrying 6 A is held directly above AB at a height of 2 mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB. [Take the value of g = 10 ms−2]
A wire AB is carrying a steady current of 6 A and is lying on the table. Another wire CD carrying 4 A is held directly above AB at a height of 1 mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB. [Take the value of g = 10 ms−2]
Draw and compare the pattern of the magnetic field lines in the two cases ?
A long solenoid of radius 2 cm has 100 turns/cm and carries a current of 5 A. A coil of radius 1 cm having 100 turns and a total resistance of 20 Ω is placed inside the solenoid coaxially. The coil is connected to a galvanometer. If the current in the solenoid is reversed in direction, find the charge flown through the galvanometer.
A circular coil of one turn of radius 5.0 cm is rotated about a diameter with a constant angular speed of 80 revolutions per minute. A uniform magnetic field B = 0.010 T exists in a direction perpendicular to the axis of rotation. Suppose the ends of the coil are connected to a resistance of 100 Ω. Neglecting the resistance of the coil, find the heat produced in the circuit in one minute.
A long solenoid is fabricated by closely winding a wire of radius 0.5 mm over a cylindrical nonmagnetic frame so that the successive turns nearly touch each other. What would be the magnetic field B at the centre of the solenoid if it carries a current of 5 A?
A tightly-wound, long solenoid is kept with its axis parallel to a large metal sheet carrying a surface current. The surface current through a width dl of the sheet is Kdl and the number of turns per unit length of the solenoid is n. The magnetic field near the centre of the solenoid is found to be zero. (a) Find the current in the solenoid. (b) If the solenoid is rotated to make its axis perpendicular to the metal sheet, what would be the magnitude of the magnetic field near its centre?
