Advertisements
Advertisements
Question
A cuboid is 8 m long, 12 m broad and 3.5 high, Find its
(i) total surface area
(ii) lateral surface area
Solution
Length of a cuboid = 8 m
The breadth of a cuboid = 12 m
Height of a cuboid = 3.5 m
(i) Total surface area = 2(lb + bh + hl)
= 2(8 x 12 + 12 x 3.5 + 3.5 x 8)
= 2(96 + 42 + 28)
= 2 x 166 = 332 m2
(ii) Lateral surface area = 2h(l + b)
= 2 x 3.5(8 + 12) = 7 x 20= 140 m2
APPEARS IN
RELATED QUESTIONS
Find the ratio of the total surface area and lateral surface area of a cube.
The dimensions of a rectangular box are in the ratio of 2 : 3 : 4 and the difference between the cost ofcovering it with sheet of paper at the rates of Rs. 8 and Rs. 9.50 per m2 is Rs.1248. Find the dimensions of the box.
Find the volume of a cuboid whose length =1.2 m, breadth = 30 cm, height = 15 cm.
An 8 m long cuboidal beam of wood when sliced produces four thousand 1 cm cubes and there is no wastage of wood in this process. If one edge of the beam is 0.5 m, find the third edge.
Find the surface area of a cuboid whose length = 6 dm, breadth = 8 dm, height = 10 dm.
Show that the product of the areas of the floor and two adjacent walls of a cuboid is the square of its volume.
A closed iron tank 12 m long, 9 m wide and 4 m deep is to be made. Determine the cost of iron sheet used at the rate of Rs 5 per metre sheet, sheet being 2 m wide.
The length of a hall is 18 m and the width 12 m. The sum of the areas of the floor and the flat roof is equal to the sum of the areas of the four walls. Find the height of the wall.
Three cubes of each side 4 cm are joined end to end. Find the surface area of the resulting cuboid.
If each edge of a cube, of volume V, is doubled, then the volume of the new cube is
If the sum of all the edges of a cube is 36 cm, then the volume (in cm3) of that cube is
If A1, A2, and A3 denote the areas of three adjacent faces of a cuboid, then its volume is
If l is the length of a diagonal of a cube of volume V, then
A cube whose volume is 1/8 cubic centimeter is placed on top of a cube whose volume is 1 cm3. The two cubes are then placed on top of a third cube whose volume is 8 cm3. The height of the stacked cubes is
The length, breadth, and height of a cuboid are in the ratio 6: 5 : 3. If its total surface area is 504 cm2; find its dimensions. Also, find the volume of the cuboid.
Find the volume of wood required to make a closed box of external dimensions 80 cm, 75 cm, and 60 cm, the thickness of walls of the box being 2 cm throughout.
The capacity of a rectangular tank is 5.2 m3 and the area of its base is 2.6 x 104 cm2; find its height (depth).
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of ₹ 10 per m2 is ₹ 15,000, find the height of the hall.
A matchbox is 4 cm long, 2.5 cm broad, and 1.5 cm in height. Its outer sides are to be covered exactly with craft paper. How much paper will be required to do so?
The length and breadth of a cuboid are 20 cm and 15 cm respectively. If its volume is 2400 cm3, find its height.
Three equal cubes of sides 5cm each are placed to form a cuboid. Find the volume and the total surface area of the cuboid.
A closed box is made of wood 5 mm thick. The external length, breadth and height of the box are 21 cm, 13 cm and 11 cm respectively. Find the volume of the wood used in making the box.
The dimensions of a hall is 10 m × 9 m × 8 m. Find the cost of white washing the walls and ceiling at the rate of ₹ 8.50 per m2
Three identical cubes of side 4 cm are joined end to end. Find the total surface area and lateral surface area of the new resulting cuboid
The total surface area of a cuboid with dimension 10 cm × 6 cm × 5 cm is
The surface area of a cuboid formed by joining two cubes of side a face to face is ______.
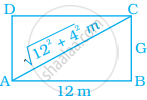
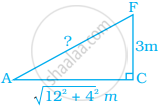
Find the length of the largest pole that can be placed in a room of dimensions 12 m × 4 m × 3 m.
External dimensions of a closed wooden box are in the ratio 5:4:3. If the cost of painting its outer surface at the rate of Rs 5 per dm2 is Rs 11,750, find the dimensions of the box.
