Advertisements
Advertisements
Question
- Determine the ‘effective focal length’ of the combination of the two lenses, if they are placed 8.0 cm apart with their principal axes coincident. Does the answer depend on which side of the combination a beam of parallel light is incident? Is the notion of the effective focal length of this system useful at all?
- An object 1.5 cm in size is placed on the side of the convex lens in the arrangement (a) above. The distance between the object and the convex lens is 40 cm. Determine the magnification produced by the two-lens system and the size of the image.
Solution
Focal length of the convex lens, f1 = 30 cm
Focal length of the concave lens, f2 = −20 cm
Distance between the two lenses, d = 8.0 cm
(a) (i) When the parallel beam of light is incident on the convex lens first:
According to the lens formula, we have:
`1/"v"_1 - 1/"u"_1 = 1/"f"_1`
Where
`"u"_1` = Object distance = ∞
v1 = Image distance
`1/"v"_1 = 1/30- 1/∞ = 1/30`
∴ v1 = 30 cm
The image will act as a virtual object for the concave lens.
Applying lens formula to the concave lens, we have:
`1/"v"_2 - 1/"u"_2 = 1/"f"_2`
Where,
`"u"_2` = Object distance
= (30 − d) = 30 − 8 = 22 cm
`"v"_2` = Image distance
`1/"v"_2 = 1/22 - 1/20 = (10-11)/220 = (-1)/220`
∴ v2 = −220 cm
The parallel incident beam appears to diverge from a point that is `(220 - "d"/2 = 220 - 4)`216 m from the centre of the combination of the two lenses.
(ii) When the parallel beam of light is incident, from the left, on the concave lens first:
According to the lens formula, we have:
`1/"v"_2 - 1/"u"_2 = 1/"f"_2`
`1/"v"_2 = 1/"f"_2 + 1/"u"_2`
Where
`"u"_2` = Object distance = −∞
`"v"_2` = Image distance
`1/"v"_2 = 1/-20 + 1/-∞ = -1/20`
∴ v2 = −20 cm
The image will act as a real object for the convex lens.
Applying lens formula to the convex lens, we have:
`1/"v"_1 - 1/"u"_1 = 1/"f"_1`
Where,
`"u"_1` = Object distance
= −(20 + d) = −(20 + 8) = −28 cm
`1/"v"_1 = 1/30 + 1/-28 = (14 - 15)/420 = (-1)/420`
∴ v2 = −420 cm
Hence, the parallel incident beam appears to diverge from a point that is (420 − 4) 416 cm from the left of the centre of the combination of the two lenses.
The answer does depend on the side of the combination at which the parallel beam of light is incident. The notion of effective focal length does not seem to be useful for this combination.
(b) Height of the image, h1 = 1.5 cm
Object distance from the side of the convex lens, `"u"_1` = −40 cm
`|"u"_1|` = 40 cm
According to the lens formula:
`1/"v"_1 - 1/"u"_1 = 1/"f"_1`
Where
`"v"_1` = Image distance
`1/"v"_1 = 1/30 + 1/(-40) = (4-3)/120 = 1/120`
∴ v1 = 120 cm
Magnification, `"m" = "v"_1/|"u"_1|`
= `120/40`
= 3
Hence, the magnification due to the convex lens is 3.
The image formed by the convex lens acts as an object for the concave lens.
According to the lens formula:
`1/"v"_2 - 1/"u"_2 = 1/"f"_2`
Where
`"u"_2` = Object distance
= +(120 − 8) = 112 cm
`"v"_2` = Image distance
`1/"v"_2 = 1/-20 + 1/112 = (-112 + 20)/2240 = (-92)/2240`
∴ v2 = `(-2240)/92` cm
Magnification, `"m'" = |"v"_2/"u"_2|`
= `2240/92 xx 1/112`
= `20/92`
Hence, the magnification due to the concave lens is `20/92`.
The magnification produced by the combination of the two lenses is calculated as: `"m" xx "m'"`
= `3 xx 20/92`
= `60/92`
= 0.652
The magnification of the combination is given as:
`"h"_2/"h"_1` = 0.652
h2 = 0.652 × h1
Where
h1 = Object size = 1.5 cm
h2 = Size of the image
∴ h2 = 0.652 × 1.5 = 0.98 cm
Hence, the height of the image is 0.98 cm.
APPEARS IN
RELATED QUESTIONS
A beam of light converges at a point P. Now a lens is placed in the path of the convergent beam 12 cm from P. At what point does the beam converge if the lens is
- a convex lens of focal length 20 cm, and
- a concave lens of focal length 16 cm?
An object of size 3.0 cm is placed 14 cm in front of a concave lens of focal length 21 cm. Describe the image produced by the lens. What happens if the object is moved further away from the lens?
You have learnt that plane and convex mirrors produce virtual images of objects. Can they produce real images under some circumstances? Explain.
A screen is placed 90 cm from an object. The image of the object on the screen is formed by a convex lens at two different locations separated by 20 cm. Determine the focal length of the lens.
A man with normal near point (25 cm) reads a book with small print using a magnifying glass: a thin convex lens of focal length 5 cm.
(a) What is the closest and the farthest distance at which he should keep the lens from the page so that he can read the book when viewing through the magnifying glass?
(b) What is the maximum and the minimum angular magnification (magnifying power) possible using the above simple microscope?
A double convex lens of + 5 D is made of glass of refractive index 1.55 with both faces of equal radii of curvature. Find the value of its radius of curvature.
Two converging lenses of unequal focal lengths can be used to reduce the aperture of a parallel beam of light without loosing the energy of the light. This increase the intensity. Describe how the converging lenses should be placed to do this.
A convex lens forms a real image of a point object placed on its principals axis. If the upper half of the lens is painted black,
(a) the image will be shifted downward
(b) the image will be shifted upward
(c) the image will not be shifted
(d) the intensity of the image will decrease.
A pin of length 2.0 cm lies along the principal axis of a converging lens, the centre being at a distance of 11 cm from the lens. The focal length of the lens is 6 cm. Find the size of the image.
An object approaches a convergent lens from the left of the lens with a uniform speed 5 m/s and stops at the focus. The image ______.
Will the focal length of a lens for red light be more, same or less than that for blue light?
An unsymmetrical double convex thin lens forms the image of a point object on its axis. Will the position of the image change if the lens is reversed?
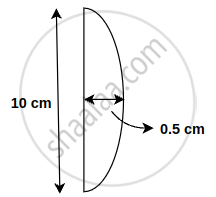
A plano convex lens has diameter of 10 cm and its thickness at the centre is 0.5 cm. Speed of light in the lens is 2 × 108 ms-1. What is the focal length of the lens?
In the given figure the radius of curvature of the curved face in the planoconvex and the planoconcave lens is 15 cm each. The refractive index of the material of the lenses is 1.5. Find the final position of the image formed.
Show that the least possible distance between an object and its real image in a convex lens is 4f, where f is the focal length of the lens.
