Advertisements
Advertisements
Question
A gas occupies 500 cm3 at a normal temperature. At what temperature will the volume of the gas be reduced by 20% of its original volume, the pressure is constant?
Solution
V = 500 cm3
Normal temperature, t = 0°C = 0 + 273 K
V1 = Reduced volume + 20% of 500 cm3
`= (20 xx 500)/100 = 100 "cm"^3`
Net, V1 = 500 - 100 = 400 cm3
T1= ?
P = P1
Using gas equation,
`"PV"/"T" = ("P"_1 "V"_1)/"T"_1`
`("P" xx 500)/273 = ("P" xx 400)/"T"_1`
T1 = `(273 xx 4)/5 = 218.4 "K"`
APPEARS IN
RELATED QUESTIONS
The figure shows the plot of PV/T versus Pfor 1.00×10–3 kg of oxygen gas at two different temperatures.
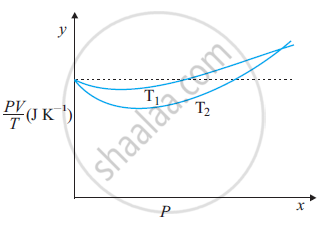
(a) What does the dotted plot signify?
(b) Which is true: T1 > T2 or T1 < T2?
(c) What is the value of PV/T where the curves meet on the y-axis?
(d) If we obtained similar plots for 1.00 ×10–3 kg of hydrogen, would we get the same value of PV/T at the point where the curves meet on the y-axis? If not, what mass of hydrogen yields the same value of PV/T (for low pressure high temperature region of the plot)? (Molecular mass of H2 = 2.02 u, of O2 = 32.0 u, R = 8.31 J mo1–1 K–1.)
What do you understand by gas?
Correct the following statement:
0°C is equal to zero Kelvin.
Name or state the following:
The standard pressure of a gas in cm. of mercury corresponding to one atmospheric pressure.
Give reason for the following:
Volumes of gases are converted into s.t.p. conditions and then compared.
Show that for diatomic gas the ratio of the two specific heats is 7:5.
Gases exert pressure on the walls of the container because the gas molecules ______
Three vessels of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monatomic), the second contains chlorine (diatomic), and the third contains uranium hexafluoride (polyatomic).
Do the vessels contain an equal number of respective molecules?
At room temperature, a diatomic gas is found to have an r.m.s. speed of 1930 ms-1. The gas is ______.
Two tanks of equal volume contain equal mass of oxygen and nitrogen at 127°C. Find the ratio of pressure in two tanks.
