Advertisements
Advertisements
Question
A man 160 cm tall, walks away from a source of light situated at the top of a pole 6 m high, at the rate of 1.1 m/sec. How fast is the length of his shadow increasing when he is 1 m away from the pole?
Advertisements
Solution
Let AB be the lamp post. Suppose at any time t, the man CD is at a distance of x km from the lamp post and y m is the length of his shadow CE.
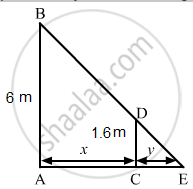
\[\text { Since triangles ABE and CDE are similar }, \]
\[\frac{AB}{CD} = \frac{AE}{CE}\]
\[ \Rightarrow \frac{6}{1 . 6} = \frac{x + y}{y}\]
\[ \Rightarrow \frac{x}{y} = \frac{6}{1 . 6} - 1\]
\[ \Rightarrow \frac{x}{y} = \frac{4 . 4}{1 . 6}\]
\[ \Rightarrow y = \frac{16}{44}x\]
\[ \Rightarrow \frac{dy}{dt} = \frac{16}{44}\left( \frac{dx}{dt} \right)\]
\[ \Rightarrow \frac{dy}{dt} = \frac{16}{44} \times 1 . 1 \left( \because \frac{dx}{dt} = 1 . 1 \right)\]
\[ \Rightarrow \frac{dy}{dt} = 0 . 4 m/\sec\]
APPEARS IN
RELATED QUESTIONS
The volume of a sphere is increasing at the rate of 8 cm3/s. Find the rate at which its surface area is increasing when the radius of the sphere is 12 cm.
The volume of a sphere is increasing at the rate of 3 cubic centimeter per second. Find the rate of increase of its surface area, when the radius is 2 cm
The total cost C(x) associated with the production of x units of an item is given by C(x) = 0.005x3 – 0.02x2 + 30x + 5000. Find the marginal cost when 3 units are produced, whereby marginal cost we mean the instantaneous rate of change of total cost at any level of output.
Find the rate of change of the volume of a sphere with respect to its diameter ?
The side of a square sheet is increasing at the rate of 4 cm per minute. At what rate is the area increasing when the side is 8 cm long?
The radius of a spherical soap bubble is increasing at the rate of 0.2 cm/sec. Find the rate of increase of its surface area, when the radius is 7 cm.
The radius of an air bubble is increasing at the rate of 0.5 cm/sec. At what rate is the volume of the bubble increasing when the radius is 1 cm?
If y = 7x − x3 and x increases at the rate of 4 units per second, how fast is the slope of the curve changing when x = 2?
The top of a ladder 6 metres long is resting against a vertical wall on a level pavement, when the ladder begins to slide outwards. At the moment when the foot of the ladder is 4 metres from the wall, it is sliding away from the wall at the rate of 0.5 m/sec. How fast is the top-sliding downwards at this instance?
How far is the foot from the wall when it and the top are moving at the same rate?
Water is running into an inverted cone at the rate of π cubic metres per minute. The height of the cone is 10 metres, and the radius of its base is 5 m. How fast the water level is rising when the water stands 7.5 m below the base.
Sand is being poured onto a conical pile at the constant rate of 50 cm3/ minute such that the height of the cone is always one half of the radius of its base. How fast is the height of the pile increasing when the sand is 5 cm deep ?
A kite is 120 m high and 130 m of string is out. If the kite is moving away horizontally at the rate of 52 m/sec, find the rate at which the string is being paid out.
A particle moves along the curve y = (2/3)x3 + 1. Find the points on the curve at which the y-coordinate is changing twice as fast as the x-coordinate ?
The volume of a cube is increasing at the rate of 9 cm3/sec. How fast is the surface area increasing when the length of an edge is 10 cm?
The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of the perimeter.
The volume of a sphere is increasing at 3 cubic centimeter per second. Find the rate of increase of the radius, when the radius is 2 cms ?
The side of a square is increasing at the rate of 0.1 cm/sec. Find the rate of increase of its perimeter ?
Find the surface area of a sphere when its volume is changing at the same rate as its radius ?
Side of an equilateral triangle expands at the rate of 2 cm/sec. The rate of increase of its area when each side is 10 cm is
The radius of a sphere is changing at the rate of 0.1 cm/sec. The rate of change of its surface area when the radius is 200 cm is
For what values of x is the rate of increase of x3 − 5x2 + 5x + 8 is twice the rate of increase of x ?
The radius of the base of a cone is increasing at the rate of 3 cm/minute and the altitude is decreasing at the rate of 4 cm/minute. The rate of change of lateral surface when the radius = 7 cm and altitude 24 cm is
The volume of a sphere is increasing at 3 cm3/sec. The rate at which the radius increases when radius is 2 cm, is
If s = t3 − 4t2 + 5 describes the motion of a particle, then its velocity when the acceleration vanishes, is
The diameter of a circle is increasing at the rate of 1 cm/sec. When its radius is π, the rate of increase of its area is
A man of height 6 ft walks at a uniform speed of 9 ft/sec from a lamp fixed at 15 ft height. The length of his shadow is increasing at the rate of
Evaluate: `int (x(1+x^2))/(1+x^4)dx`
A kite is moving horizontally at a height of 151.5 meters. If the speed of kite is 10 m/s, how fast is the string being let out; when the kite is 250 m away from the boy who is flying the kite? The height of boy is 1.5 m.
The rate of change of volume of a sphere is equal to the rate of change of the radius than its radius equal to ____________.
If the rate of change of volume of a sphere is equal to the rate of change of its radius then the surface area of a sphere is ____________.
Let y = f(x) be a function. If the change in one quantity 'y’ varies with another quantity x, then which of the following denote the rate of change of y with respect to x.
A spherical balloon is filled with 4500π cubic meters of helium gas. If a leak in the balloon causes the gas to escape at the rate of 72π cubic meters per minute, then the rate (in meters per minute) at which the radius of the balloon decreases 49 minutes after the leakage began is ______.
The median of an equilateral triangle is increasing at the ratio of `2sqrt(3)` cm/s. Find the rate at which its side is increasing.
What does evaluating \[\left.\frac{dy}{dx}\right|_{x=x_0}\] give?
For the Chain Rule for Rates \[\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}\], which condition is required?
For a circle with area \[A=\pi r^2\], what is \[\frac{dA}{dr}\]?
For \[\text{C}(x)=0.005x^3-0.02x^2+30x+5000\], what is the marginal cost when \[x=3\]?
What does a negative derivative mean for a quantity?
