Advertisements
Advertisements
Question
A parallel plate capacitor is filled by a dielectric whose relative permittivity varies with the applied voltage (U) as ε = αU where α = 2V–1. A similar capacitor with no dielectric is charged to U0 = 78V. It is then connected to the uncharged capacitor with the dielectric. Find the final voltage on the capacitors.
Solution
Let the final voltage be U: If C is the capacitance of the capacitor without the dielectric, then the charge on the capacitor is
Q1 = CU
The capacitor with the dielectric has a capacitance εC. Hence the charge on the capacitor is
Q2 = εU = α CU2
The initial charge on the capacitor that was charged is
Q0 = CU0
From the conservation of charges,
Q0 = Q1 + Q2
Or, CU0 = CU + α CU2
⇒ αU2 + U – u0 = 0
∴ U = `(-1 +- sqrt(1 + 4αU_0))/(2α)`
= `(-1 +- sqrt(1 + 624))/4`
= `(-1 +- sqrt(625))/4` volts
As U is positive
U = `(sqrt(625) - 1)/4 = 24/4` = 6V
APPEARS IN
RELATED QUESTIONS
A spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports. Show that the capacitance of a spherical capacitor is given by
C = `(4piin_0"r"_1"r"_2)/("r"_1 - "r"_2)`

where r1 and r2 are the radii of outer and inner spheres, respectively.
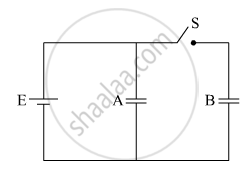
Two identical parallel plate capacitors A and B are connected to a battery of V volts with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant K. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.
(i) Find equivalent capacitance between A and B in the combination given below. Each capacitor is of 2 µF capacitance.
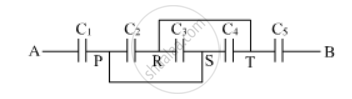
(ii) If a dc source of 7 V is connected across AB, how much charge is drawn from the source and what is the energy stored in the network?
Two conducting spheres of radii R1 and R2 are kept widely separated from each other. What are their individual capacitances? If the spheres are connected by a metal wire, what will be the capacitance of the combination? Think in terms of series−parallel connections.
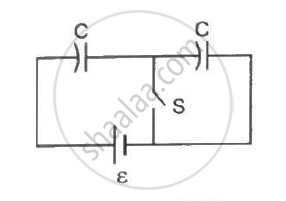
Consider the situation shown in the figure. The switch S is open for a long time and then closed. (a) Find the charge flown through the battery when the switch S is closed. (b) Find the work done by the battery.(c) Find the change in energy stored in the capacitors.(d) Find the heat developed in the system.
The separation between the plates of a parallel-plate capacitor is 0⋅500 cm and its plate area is 100 cm2. A 0⋅400 cm thick metal plate is inserted into the gap with its faces parallel to the plates. Show that the capacitance of the assembly is independent of the position of the metal plate within the gap and find its value.
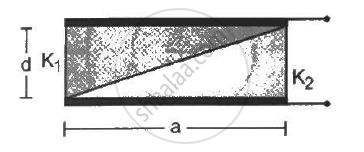
A capacitor is formed by two square metal-plates of edge a, separated by a distance d. Dielectrics of dielectric constant K1 and K2 are filled in the gap as shown in figure . Find the capacitance.
Three capacitors C1 = 3μF, C2 = 6μF, and C3 = 10μF are connected to a 50 V battery as shown in Figure below:

Calculate:
(i) The equivalent capacitance of the circuit between points A and B.
(ii) The charge on C1.
Derive the expression for resultant capacitance, when the capacitor is connected in series.
The displacement current of 4.425 µA is developed in the space between the plates of the parallel plate capacitor when voltage is changing at a rate of 106 Vs-1. The area of each plate of the capacitor is 40 cm2. The distance between each plate of the capacitor is x × 10-3 m. The value of x is ______.
(Permittivity of free space, ε0 = 8.85 × 10-12C2N-1m-2).
